|
Question 110759: WRite the equation of the line passing through (4,-25) and (-3, 17).
Thank you.
Found 2 solutions by stanbon, jim_thompson5910:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! WRite the equation of the line passing through (4,-25) and (-3, 17).
--------------
slope = [-25-17]/[4--3] = -42/7 = -6
------------------
Use y=mx+b and substitute to find "b".
-25 = 6*4 + b
b = -49
--------------
EQUATION:
y = 6x -49
================
Cheers,
Stan H.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: Start with the slope formula (note: ) is the first point ( is the first point ( , , ) and ) and ) is the second point ( is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 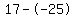 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 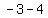 to get to get 
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and is the slope, and ) is one of the given points is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 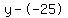 as as 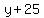
 Distribute Distribute 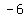
 Multiply Multiply 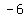 and and  to get to get 
 Subtract Subtract  from both sides to isolate y from both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
|
|
| |