Question 1106950: can you plot this on a coordinate plane?
{y=1/2x+4
{x+4y=4
Found 2 solutions by Boreal, KMST:
Answer by Boreal(15235)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I can, and I could tell you how I do it.
Equation like
 , ,  , ,  , and , and  , ,
are called linear equations for a good reason:
their graphs are straight lines.
Two points determine a line,
so all you need to plot one of those equations
is to find two pairs of coordinates that satisfy the equation,
plot them as two points on graph paper,
and connect the points with a straight line.
You could find and plot more than two points, but it is not necessary.
Look at  . .
You realize that when  , ,  , so , so  . .
That gives you point 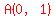 . .
Also, when  , ,  . .
That gives you point  . .
Plotting the points, and connecting them, you have

Now, look at  . .
For  you get you get  , which gives you point , which gives you point 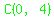 . .
For  you get you get  . .
That gives you point 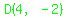 . .
Adding those two points, and the line connecting them, you have
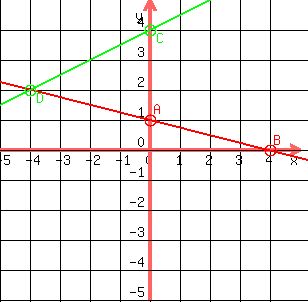
The two lines seem to intersect at 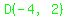 , which happened to be , which happened to be
a point that we had calculated for  . .
That seems to be a solution of the system of linear equations
 . .
We know that point 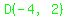 is part of is part of  , ,
but we should confirm that it is also part of  . .
For  , when , when  and and 
 , so , so  or or 
indeed satisfies both equations,
meaning that it is the solution for system
 . .
|
|
|