|
Question 1101052: Triangle ABC is isosceles with AB=BC=10 units and apex B (1,8). The base AC is parallel to the x-axis. D (1,2) is a point on AC such that BD is perpendicular to AC.
a. Find the coordinates of A and C.
b. Find the area of triangle ABC.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is what the triangle looks like, with all the listed points and line segments:

a. The coordinates of A and C, could be 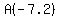 and and 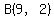 , ,
as I labeled them,
or they could be 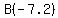 and and 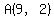 . .
I know the coordinates of the points,
but I do not know if the person who gave those points their names
started naming them clockwise from bottom left, or counterclockwise from bottom right.
b. The area of triangle ABC is 48 square units.
HOW DO I KNOW:
I will "show my work", although I did all that work in my head.
I would like to use side AC as the base of the triangle.
Line segment BD, perpendicular to base AC from vertex B,
is obviously the altitude with respect to base AC.
Its length is the height of the triangle.
Since B and D have both have the same x-coordinate,
the length of BD is the difference of their y-coordinates.
So  . .
Segment BD divides ABC into two congruent right triangles: triangle ADB and triangle CDB.
 is one leg of right triangle ADB. is one leg of right triangle ADB.
 is the hypotenuse, and is the hypotenuse, and
 is the other leg. is the other leg.
Because it is a right triangle we could use the Pythagorean theorem.
I did not go through that trouble,
because I recognized triangle ADB as a 6-8-10 right triangle,
one with sides measuring 6, 9, 10.
(Teachers like to use 3-4-5, 6-8-10, 9-12-15, ... right triangles
because they remember that the 3:4:5 ratio gives you a right triangle
with integer side lengths).
Using the Pythagorean theorem, I would show my work by writing






 . .
As we know that ADB and CDB are congruent right triangles,
we know that  , ,
because Corresponding Parts of Congruent Triangles are Congruent (which teachers abbreviate as CPCTC).
So we know that A and C are at 8 unit distance to either side of D,
on the line parallel to the x-axis that goes through D,
and that is the line  . .
So, the y-coordinate of A and C is  , ,
and the x-coordinates of those two points
have a difference of  from the x-coordinate of from the x-coordinate of 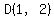 . .
Hence, A and C have  . .
I had to make a choice, so I assigned  to A and to A and  to C. to C.
The area of a triangle is calculated as
 , ,
so I calculated it as  . .
I could have written  and and
 , ,
but I just calculated it my way in my head so as not to waste time and paper.
NOTE:
We did not need all the information given.
We were told that B is 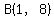 and that: and that:
1) AC is parallel to the x-axis,
2) BD is perpendicular to AC, and
3) the coordinates of D are and 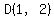 . .
Any two of those statements allows you to figure out the remaining statement.,
however, it is nice to have one less thing to figure out.
|
|
|
| |