|
Question 1098453: Use the graphic method to solve this problem
Minimize the objective function:
3x+2y
Subject to the constraints:
2x+y>=30
2x+5y>=50
x+y=>20
x>=0
y>=0
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The feasible region is presented in the plot below.
It is the region in the first quadrant above the given straight lines - the constraints.
 The lines 2x+y = 30 (red), 2x+5y = 50 (green) and x+y = 20 (blue).
This region has vertices P1, P2, P3 and P4
P1 = (0,30), which is y-intercept of the red line 2x+y = 30;
P2 = (10,10), which is the intersection point of the red line 2x+y = 30 and blue line x+y = 20;
P3 = (
The lines 2x+y = 30 (red), 2x+5y = 50 (green) and x+y = 20 (blue).
This region has vertices P1, P2, P3 and P4
P1 = (0,30), which is y-intercept of the red line 2x+y = 30;
P2 = (10,10), which is the intersection point of the red line 2x+y = 30 and blue line x+y = 20;
P3 = ( , ,  ), which is the intersection point of the blue line x+y = 20 and green line 2x+5y = 50;
P4 = (25,0), which is x-intercept of the green line 2x+5y = 50.
The graphic Linear Programming method includes finding the intersection points as the solutions of given constraint equations; these
procedures are considered as of atomic size components, and it is assumed that the student makes them automatically without special discussions.
Further, the Linear Programming method enact you to calculate the values of the objective function F(x,y) = 3x + 2y at the vertices
at P1: F( 0,30) = 3*0 + 2*30 = 60;
at P2: F(10,10) = 3*10 + 2*10 = 50;
at P3: F( ), which is the intersection point of the blue line x+y = 20 and green line 2x+5y = 50;
P4 = (25,0), which is x-intercept of the green line 2x+5y = 50.
The graphic Linear Programming method includes finding the intersection points as the solutions of given constraint equations; these
procedures are considered as of atomic size components, and it is assumed that the student makes them automatically without special discussions.
Further, the Linear Programming method enact you to calculate the values of the objective function F(x,y) = 3x + 2y at the vertices
at P1: F( 0,30) = 3*0 + 2*30 = 60;
at P2: F(10,10) = 3*10 + 2*10 = 50;
at P3: F( , , ) = ) = 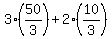 = =   ;
at P4: F(25,0) = 3*25 + 2*0 = 75.
Then the Linear Programming method STATES that the objective function in the feasible region achieves its minimum
at the vertex; namely at that vertex, where its value is minimal.
From the list above, the objective function has the minimum at P2 = (10,10), and this point is the minimum of the objective function
over the entire feasible region.
Thus the solution of the problem is the point P2 = (10,10).
It means that the objective function under the given constraints achieves its minimum at the point x = 10, y = 10.
The value of this minimum is ;
at P4: F(25,0) = 3*25 + 2*0 = 75.
Then the Linear Programming method STATES that the objective function in the feasible region achieves its minimum
at the vertex; namely at that vertex, where its value is minimal.
From the list above, the objective function has the minimum at P2 = (10,10), and this point is the minimum of the objective function
over the entire feasible region.
Thus the solution of the problem is the point P2 = (10,10).
It means that the objective function under the given constraints achieves its minimum at the point x = 10, y = 10.
The value of this minimum is 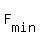 = 50.
Answer. The objective function under the given constraints achieves its minimum at the point x = 10, y = 10.
The value of this minimum is = 50.
Answer. The objective function under the given constraints achieves its minimum at the point x = 10, y = 10.
The value of this minimum is 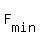 = 50. = 50.
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The solution you got from tutor ikleyn was very well done and very thorough.
However, there is a shortcut for getting to the final answer, without having to evaluate the objective function at all the vertices of the feasibility region. In fact, with this shortcut it is not even necessary to find all the vertices of the feasibility region.
I will refer to her response in describing the shortcut.
The slopes of the three constraint lines are -2 (red), -1 (blue), and -2/5 (green).
The objective function, evaluated at some particular point, is 3x+2y equal to some number. All lines with equations of that form have slopes of -3/2.
We need to find where a line with slope -3/2 touches a single vertex of the feasibility region, and does not pass through any portion of the feasibility region.
If you think about that, it is going to occur at the vertex where the slope of the objective function is between the slopes of the two intersecting constraint functions.
Since the slope of the objective function, -3/2, is between -2 and -1 (the intersection of the red and blue lines), that vertex is where the minimum value of the objective function is going to occur.
So the vertex where the minimum value of the objective function occurs is the intersection of the red and blue lines.
The only vertex of the feasibility region for which you need to determine the coordinates is that one; and then the minimum value of the objective function is the objective function evaluated at those coordinates.
So the streamlined process for solving this kind of problem is
(1) Find the slopes of the constraint lines and of the objective function;
(2) Find the two constraint lines for which the slope of the objective function is between the slopes of the two constraint lines;
(3) Find the coordinates of the intersection of those two constraint lines; and
(4) Evaluate the objective function at that point.
|
|
|
| |