Write that as a matrix by dropping the letters
and putting vertical line instead of equal signs:
The idea is to get three zeros in the three positions
in the lower left corner of the matrix, where the elements
I've colored red are:
To get a 0 where the red 2 on the left of the middle row is,
multiply R1 by -2 and add it to 1 times R2, and put it in place
of the present R2. That's written as
-2R1+1R2->R2
To make it easy, write the multipliers to the left of the two
rows you're working with; that is, put a -2 by R1 and a 1 by R2
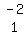
We are going to change only R2. Although R1 gets multiplied
by -2 we are going to just do that mentally and add it to R2, but
not really change R1.
Since it just happens that row 2 can be divided through by 3,
without getting fractions, let's do it. We multiply row 2 by
1/3. That operation is written
R2->R2
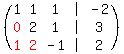To get a 0 where the lower left red 1 is, multiply R1
by -1 and add it to 1 times R3. That's written as
-1R1+1R3->R3
Write the multipliers to the left of the two rows you're
working with; that is, put a -1 by R1 and a 1 by R3
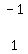
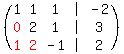We are going to change only R3.
It will be more convenient to get a 1 where the 2 is,
so we swap rows 2 and 3. This is written
R2<->R3
To get a 0 where the red 2 is, multiply R2
by -2 and add it to R3. That's written as
-2R2+R3->R3
Write the multipliers to the left of the two
rows you're working with; that is, put a -2 by R2 and a 1 by R3
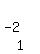
We are going to change only R3.
Since it just happens that row 3 can be divided through by 5,
without getting fractions, let's do it. We multiply row 3 by
1/5. That operation is written
R3<->R3
Now that we have 0's in the three positions in the
lower left corner of the matrix, we change the matrix
back to equations:
he third equation gives us f
Substitute -1 for z in the middle equation:
Substitute -1 for z and 2 for y in the top equation:
So the solution is 
Edwin
