|
Question 1091624: Ramesh and Narendra start from the same place and arrive at another place in 40 minutes and 60 minutes respectively.
If Narendra starts 10 minute earlier than Ramesh, how much time Ramesh will take to reach Narendra.
Found 3 solutions by richwmiller, ikleyn, MathTherapy:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by ikleyn(52784)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ramesh and Narendra start from the same place and arrive at another place in 40 minutes and 60 minutes respectively.
If Narendra starts 10 minute earlier than Ramesh, how much time Ramesh will take to reach Narendra.
Let distance traveled to "another place," be D
Then Ramesh’s speed = 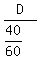 , or , or 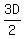
Also, Narendra’s speed = 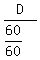 , or D , or D
Let time it takes Ramesh to reach Narendra (get to catch-up point), be T
Then Narendra’s time to get to catch-up point = 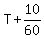 , or , or 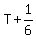
We then get the following DISTANCE equation: 

9DT = 6DT + D -------- Multiplying by LCD, 6
9DT – 6DT = D
3DT = D
T, or time Ramesh takes to catch up to Narendra, if Narendra leaves 10 minutes before Ramesh = 
****Note: You failed to mention that when they left the SAME PLACE, they did so at the SAME TIME.
So, it should be:: Ramesh and Narendra start from the same place AT THE SAME TIME and arrive at another place in 40 minutes and 60 minutes respectively.
I don't have to, because I already read it. English is my 1st language and I've been learning, speaking, and writing it for 30+ years now. I do understand
English quite well, and for the most part am able to understand, decipher, and sometimes even correct others on math problems. I did the problem the way I
understand it, and unless someone can prove to me that I misinterpreted the question that was asked, I stand by my answer, 100%.
Yes, Narendra starts 10 minutes before Ramesh, and gets to the catch up point in 30 minutes, while Ramesh takes 20 (30 - 10) minutes to get to the catch-point.
What I'll do is use REAL numbers to illustrate this!
Let Narendra's speed be 50 kmh
Then Ramesh's is 1.5(50), or 75 kmh (Ramesh speed is  of Narendra's) of Narendra's)
In 60 minutes, or 1 hour Narendra completed the trip, and so the distance = 50(1), or 50 km
In 40 minutes, or  , or , or  hr, Ramesh completed hr, Ramesh completed 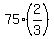 = 50 km = 50 km
Note that that was what was given (The faster Ramesh completed the trip, in 20 minutes less time than Narendra)
This makes sense, since Narendra CAN NEVER catch-up with Ramesh when they leave at the same time. But, if Narendra leaves 10 minutes before Ramesh, then they will meet at some point.
Now, 10 minutes after leaving, Narendra will have traveled: 
At this time, Ramesh leaves, and Narendra will be 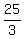 km ahead of Ramesh km ahead of Ramesh
Therefore, 20 minutes after this, Narendra will have traveled another: 
Therefore Narendra will have traveled a total of: 
In the meantime, during the 20 minutes that have elapsed since Ramesh left, Ramesh will have covered 
As seen, 30 minutes after Narendra left, she covered 25 km, and 20 minutes after Ramesh left, he also covered 25 km. The 25 km is the catch-up point.
|
|
|
| |