|
Question 1082934: Find the equation of the line passing through the point (3,4) which cuts from the first quadrant of a triangle of minimum area.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! The general point slope form of a linear equation is 
where  is the slope and is the slope and ) is the point the line goes through. is the point the line goes through.
----------------------------------------------------------
We don't know the slope m, but we do know that
=(3,4))
So,
 and and 
----------------------------------------------------------
Plugging these x and y values into the point slope formula yields


Let's solve for y



----------------------------------------------------------
In order for this line to form a triangle in quadrant 1, the slope m must be negative. So m < 0. If m > 0 then we end up with an unbounded figure of infinite area.
If m < 0, then  forms a triangle with base b and height h. The area of the triangle is A = (b*h)/2. We need to find the base and height. forms a triangle with base b and height h. The area of the triangle is A = (b*h)/2. We need to find the base and height.
To find the height h, plug in x = 0 to find the y intercept




We stop here because we don't know m yet. If we did, we can replace m with the value and simplify.
So the y intercept is the point ) where m is is some negative number. where m is is some negative number.
So the height is 
----------------------------------------------------------
To find the base b, we plug in y = 0 and solve for x. This yields the x intercept. The horizontal distance from the origin to the x intercept is equal to the base b.









The x intercept is ) where m is is some negative number. where m is is some negative number.
The base is 
----------------------------------------------------------
From the last two sections above, we found the following
base = 
height = 
The area of the triangle is therefore






----------------------------------------------------------
Replace the A with f(x). Replace the m with x. We end up with this function.

Graphing said function produces

Image generated by GeoGebra (free graphing software).
Now recall that 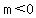 . Because we replaced m with x, this means that . Because we replaced m with x, this means that  . Only focus on the portion that is to the left of the vertical y axis. . Only focus on the portion that is to the left of the vertical y axis.
Use your calculator's "minimum" feature to find that the min point on the interval (-infinity, 0) is the point (-4/3, 24).
Note: -4/3 = -1.33 approximately.
The point P = (-1.33, 24) is marked on the graph above as that minimum point.
So  is the slope which produces the smallest area 24. is the slope which produces the smallest area 24.
-----------------------------------------------------------
Plug in  and simplify and simplify





-----------------------------------------------------------
-----------------------------------------------------------
The final answer is 
|
|
|
| |