Find the remainder when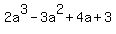 
is synthetically divided by a + 
.
Change the sign of the to 
|2 -3 4 3
|
Bring down the 2
|2 -3 4 3
|
2
Multiply the 2 by the to get -1
Write -1 above and to the right of the 2:
|2 -3 4 3
| -1
2
Combine the -3 and the -1, getting -4.
Write -4 at the bottom beside the 2
|2 -3 4 3
| 1
2 -4
Multiply the -4 by the to get -2
Write -2 above and to the right of the -4:
|2 -3 4 3
| 1 -2
2 -4
Combine the 4 and the -2, getting 2.
Write 2 at the bottom beside the -4:
|2 -3 4 3
| 1 -2
2 -4 2
Multiply the 2 by the to get -1
Write -1 above and to the right of the 2:
|2 -3 4 3
| 1 -2 -1
2 -4 2
Combine the 3 and the -1, getting 2.
Write 2 at the bottom beside the 2:
|2 -3 4 3
| 1 -2 -1
2 -4 2 2
The synthetic division is now complete,
and the remainder is the right-most term
on the bottom line. So the answer is 2.
The quotient is gotten from the first three
numbers on the bottom line and is interpreted
as
2x² - 4x + 2.
But you were only asked to give the remainder
which is the right-most number on the
bottom line of the synthetic division. So
the answer is 2.
Edwin
