Question 1077589: Find a point on the line  that is equidistant from that is equidistant from
point (3,8) and (9,6)
Found 3 solutions by josgarithmetic, Edwin McCravy, ikleyn:
Answer by josgarithmetic(39631)   (Show Source): (Show Source):
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Instead of just doing it for you, I'll do one exactly like yours,
explaining step by step for you to follow.
Find a point on the line  that is equidistant from
point (4,7) and (8,5) that is equidistant from
point (4,7) and (8,5)
 We let the point that's equidistant be (x,y).
We set the lengths of the two green lines equal. That is,
we set distance from (4,7) to (x,y) equal to the
distance from (8,5) to (x,y).
We use the distance formula:
We let the point that's equidistant be (x,y).
We set the lengths of the two green lines equal. That is,
we set distance from (4,7) to (x,y) equal to the
distance from (8,5) to (x,y).
We use the distance formula:
  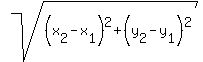
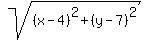  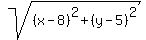 Squaring both sides:
Squaring both sides:
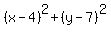  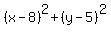
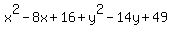  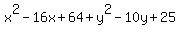 The x² and the y² terms cancel on both sides:
The x² and the y² terms cancel on both sides:
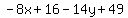  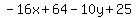 Combining the numbers
Combining the numbers
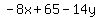  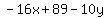 We get x and y terms on the left and a number on the right:
We get x and y terms on the left and a number on the right:
   We can divide that equation through by 4
We can divide that equation through by 4
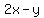   Now we have the system of equations consisting of
that equation and the given equation of the line:
Now we have the system of equations consisting of
that equation and the given equation of the line:
 Solve by elimination:
To cancel the x's, multiply the second equation
by -2
Solve by elimination:
To cancel the x's, multiply the second equation
by -2
 Adding the two equations,
matrix(1,3,-7y,""="",-12),
matrix(1,3,y,""="",12/7)))}}}
Since that came out a fraction, instead of substituting
it back, start over and eliminate the other letter:
To cancel the y's, multiply the first equation
by 3
Adding the two equations,
matrix(1,3,-7y,""="",-12),
matrix(1,3,y,""="",12/7)))}}}
Since that came out a fraction, instead of substituting
it back, start over and eliminate the other letter:
To cancel the y's, multiply the first equation
by 3
 Adding the two equations,
matrix(1,3,7x,""="",27),
matrix(1,3,y,""="",27/7)))}}}
So the desired point on the line is the point
Adding the two equations,
matrix(1,3,7x,""="",27),
matrix(1,3,y,""="",27/7)))}}}
So the desired point on the line is the point
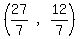 Now do yours exactly the same way, step by step.
Only the numbers will be different.
[Your answer will come out to be fractions also
with the denominator 7, but the numerators will
be different from this answer.]
Edwin
Now do yours exactly the same way, step by step.
Only the numbers will be different.
[Your answer will come out to be fractions also
with the denominator 7, but the numerators will
be different from this answer.]
Edwin
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find a point on the line  that is equidistant from that is equidistant from
point (3,8) and (9,6)
~~~~~~~~~~~~~~~~~~~~~~~~~
There is more simple / more easy way.
The locus of the points equidistant from two given points is the perpendicular bisector to the segment connecting these points.
So, what you need to do is to construct the perpendicular bisector to the segment connecting (3,8) and (9,6), and then
find its intersection with the given straight line.
The midpoint between the two given points is (6,7).
The segment connecting (3,8) and (9,6) has the slope 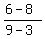 = = 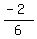 = =  .
Hence, the perpendicular line (perpendicular bisector) has the slope 3.
The line with the slope 3 passing through the point (6,7) has the equation
y - 7 = 3*(x-6), or
y = 3x -11.
The intersection of the straight lines
x + 2y = 8 (1) and
y = 3x-1 (2)
is (solve the system by substitution) the point (x,y) = ( .
Hence, the perpendicular line (perpendicular bisector) has the slope 3.
The line with the slope 3 passing through the point (6,7) has the equation
y - 7 = 3*(x-6), or
y = 3x -11.
The intersection of the straight lines
x + 2y = 8 (1) and
y = 3x-1 (2)
is (solve the system by substitution) the point (x,y) = (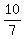 , ,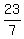 ). ).
That's all. The problem is solved. Your point is (x,y) = (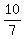 , ,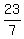 ). ).
|
|
|