|
Question 1077257: how to solve the linear equations by graphing?
y=4x+2 y=x+17
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! y=4x+2 y=x+17
y=4x+2 y=x+17
First equation: Point (0,2), slope 4
Second equation: Point (0,17), slope 1
Plot each point and use slope to form/make the line.
Read the intersection point.
Looks like near or at (4,22), but you can do some simple algebra steps to calculate the actual values.
(4x+2=x+17=y, and find x....)
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! To solve the linear equations by graphing, you
1) plot both equations on the same graph
2) find the coordinates of the intersection point
3) verify that the pair (x,y) of coordinates found is a solution of both equations
1) The graph for a linear equation is a straight line.
To draw it you just need to know two points.
The graph for  obviously passes through point  .
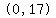Substituting a value for x in the equation, you can get another point.
Picking  , you get  ,
so 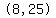 is another point in the graph of .
To get the graph of ,
you plot those two points and connect them with a straight line.
Similarly, for  you could use point  ,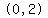
and point  .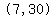
The graph for 
could look like this:
2) The lines seem to cross at point  with  .
3) substituting  into the two equations, we get
 and  ,
which verifies 
as the solution to the system of linear equations.
|
|
|
| |
