|
Question 1071358: Copperfield Mining Company owns two mines, each of which produces three grades of ore high, medium, and low. The company has a contract to supply a smelting company with at least 12 tons of high-grade ore, 8 tons of medium-grade ore, and 24 tons of low-grade ore. Each mine produces a certain amount of each type of ore during each hour that it operates. Mine 1 produces 6 tons of high-grade ore, 2 tons of medium-grade ore, and 4 tons of low-grade ore per hour. Mine 2 produces 2, 2, and 12 tons, respectively, of high-, medium-, and low-grade ore per hour. It costs Copperfield $200 per hour to mine each ton of ore from mine 1, and it costs $160 per hour to mine each ton of ore from mine 2. The company wants to determine the number of hours it needs to operate each mine so that its contractual obligations can be met at the lowest cost.
a. Formulate a linear programming model for this problem.
b. Solve this model by using graphical analysis.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the company has a contract to deliver:
at least 12 tons of high grade ore.
at least 8 tons of medium grade ore.
at least 24 tons of low grade ore.
for each hour of operation, mine 1 produces:
6 tons of high grade ore
2 tons of medium grade ore
4 tons of low grade ore
for each hour of operation, mine 2 produces:
2 tons of high grade ore
2 tons of medium grade ore
12 tons of low grade ore.
it costs $200 per hour to mine each ton of ore from mine 1.
it costs $160 per hour to mine each ton of ore from mine 2.
let x = the number of hours that mine 1 operates.
let y = the number of hours that mine 2 operates.
your cost function appears to be related to number of tons of ore produced from the mine for each hour that it operates.
we'll work on the constraints first and then worry about what the objective function needs to be.
your constraints, as far as i can determine are:
x >= 0
y >= 0
this is because the number of hours that each mine works can't be negative.
6x + 2y >= 12
this is because mine 1 can extract 6 tons of high grade ore and mine 2 can extract 2 tons of high grade ore for each hour of operation, and the number of tons of high grade ore produced has to be greater than or equal to 12.
2x + 2y >= 8
this is because mine 1 can extract 2 tons of medium grade ore and mine 2 can extract 2 tons of medium grade ore for each hour of operation, and the number of tons of medium grade ore produced has to be greater than or equal to 8.
4x + 12y >= 24
this is because mine 1 can extract 4 tons of low grade ore and mine 2 can extract 12 tons of low grade ore for each hour of operation, and the number of tons of low grade ore produced has to be greater than or equal to 24.
to summarize, your constraint functions are:
x >= 0
y >= 0
6x + 2y >= 12
2x + 2y >= 8
4x + 12y >= 24
using www.desmos.com/calculator graphing calculator, you would graph the opposite of these functions.
specifically, you would graph:
x <= 0
y <= 0
6x + 2y <= 12
2x + 2y <= 8
4x + 12y <= 24
the area of the graph that is NOT shaded is your region of feasibility.
the corner points of this region are where the max/min objective function results will be found.
your graph looks like this:
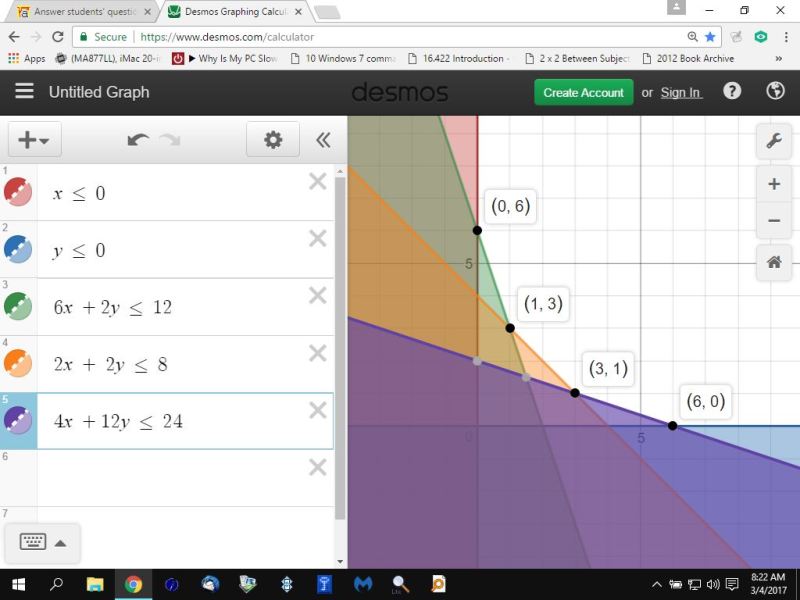
your lowest cost will be at the corner points of the feasible region, which is the area of the graph that is not shaded.
note that the feasible region has lower bounds, but does not have upper bounds.
since you are looking for the lowest cost, this is perfectly all right and you can just find the lower bounds and not worry about any upper bounds.
those corner points have been identified as (0,6), (1,3), (3,1) (6,0).
now to determine what the objective function should be.
you state that:
It costs Copperfield $200 per hour to mine each ton of ore from mine 1, and it costs $160 per hour to mine each ton of ore from mine 2
This can be translated to say:
It costs Copperfield $200 per hour per ton to operate from mine 1, and it costs Copperfield $160 per hour per ton to operate from mine 2.
you also state that:
Mine 1 produces 6 tons of high-grade ore, 2 tons of medium-grade ore, and 4 tons of low-grade ore per hour.
Mine 2 produces 2 tons of high grade ore, 2 tons of medium-grade ore, and 12 tons of low-grade ore per hour.
this leads me to believe that the total costs for mine 1 to operate would be:
$200 * (6 + 2 + 4) = $200 * 12 = $2400 per hour.
and the total costs for mine 2 to operate would be:
$160 * (2 + 2 + 12) = $160 * 16 = $2560 per hour.
your objective function would therefore be:
cost = 2400x + 2560y
at each of the corner points, your total cost would be:
when x = 0 and y = 6, total costs = 0 * 2400 + 6 * 2560 = 15360
when x = 1 and y = 3, total costs = 1 * 2400 + 3 * 2560 = 10080
when x = 3 and y = 1, total costs = 3 * 2400 + 1 * 2560 = 9760
when x = 6 and y = 0, total costs = 6 * 2400 + 0 * 2560 = 14400
minimum cost of operation is when x = 3 and y = 1.
when x = 3 and y = 1
total cost = 3 * 2400 + 1 * 2560 = 9760
tons of high grade ore produced = 3 * 6 + 1 * 2 = 20 which is >= 12
tons of medium grade ore produced = 3 * 2 + 1 * 2 = 8 which is >= 8
tons of low grade ore produced = 6 * 4 + 1 * 12 = 36 which is >= 24
all the constraints are met, and even exceeded, at minimal cost to the company.
the biggest problem i had was understanding what the cost function should be.
it took me a little while to understand that, for each hour of operation, the mine produced several tons of ore and that the total cost per hour for the operation of that mine had to be dollars per hour per ton produced and not just dollars per hour.
i think i got it right.
hopefully you, and more importantly, your instructor, agree.
|
|
|
| |