Question 1070873: The second term and the fifth term of a geometric series are 3 and 81 respectively. Find the sum from the fifth term to the tenth term of this series.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Mental math says that the common ratio is  . .
With formulas, id  is the first term, is the first term,
and  is the common ratio, is the common ratio,
 , so , so
 is is 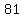 , the fifth term, , the fifth term,
 is is  , the second term, , the second term,
 , ,
 , and substituting , and substituting
 , ,
 , ,
 , and , and  . .
The sum of  terms starting from a term terms starting from a term 
in a geometric series with common ratio  , is , is
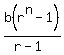 . .
We are skipping the first  terms of a geometric series with terms of a geometric series with  , ,
and adding up the next  terms, terms,
starting from fifth term  and adding up to the tenth term, and adding up to the tenth term,
so the sum is

You may think that I need to find the first term of that series,
then calculate the sum of the first 10 terms,
next calculate the sum of the first 4 terms,
and finally subtract one sum from the other.
That is inefficient.
Who can say that I am not allowed to think of my own series,
which happens to have the same  as the series in the problem, as the series in the problem,
and the same terms, except for missing the first 4?
|
|
|