.
First part of the condition says
x + y + z = 243, (1)
where x is the first quantity, y is the second and z is the third.
Second part of the condition gives these equalities
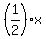 =
=  , (2)
, (2)
 =
= 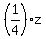 (3)
From (2), y =
(3)
From (2), y = 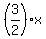 , z =
, z =  =
= 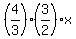 = 2x.
Substitute it into (3), and you will get
= 2x.
Substitute it into (3), and you will get
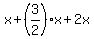 = 243, or
4.5x = 243.
x =
= 243, or
4.5x = 243.
x = 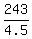 = 54.
Then y =
= 54.
Then y = 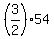 = 81 and z = 2x = 108.
= 81 and z = 2x = 108.