SOLUTION: Find the value of K for the followibg pair of linear equation have infinetly many solution :— x+(k+1)y=5 (k+1)x+9y=8y-1

x      + (k+1)y = 5,         (1)
(k+1)x +     9y = 8y - 1.    (2)

is equivalent to 

x      + (k+1)y =  5,        (1')
(k+1)x +      y = -1.        (2')

The theory says: 

   - if the determinant of the matrix of the system is not zero, then the solution is unique.

   - if the determinant of the matrix of the system is zero,     then two options are possible: 

     1) there is NO solution,  OR  2) there are infinitely many solutions.

The determinant of the matrix is

     det  =  = .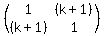

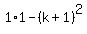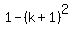The condition det = 0 is this equation for "k"

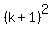 = 1,

which has these two solutions: 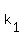  = 0, 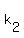   = -2.


At k = 0 the system (1'), (2') is 

 x + y =  5,     
 x + y = -1

and has NO solutions. 


At k = -2 the system (1'), (2') is 

 x - y =  5,     
-x + y = -1

and has NO solutions, again.