|
Question 1050488: Write the slope-intercept equation of the function f whose graph satisifies the given conditions.
The graph of f passes through
left parenthesis negative 4 comma 8 right parenthesis(−4,8)
and is perpendicular to the line that has an x-intercept of
11
and a y-intercept of
negative 2−2.
Found 3 solutions by ewatrrr, Boreal, MathTherapy:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi
Original Line:
(11, 0)
(0,-2) m = 2/11 m =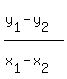
Line Perpendicular to that Line: m = -11/2 (negative reciprocal)
Perpendicular Line passes thru (-4, 8)
y - 8 = (-11/2)(x + 4) ***Using point-slope form, 
y = (-11/2)x -22 + 8
y = (-11/2)x - 14 (slope-intercept form)
Answer by Boreal(15235)  (Show Source):
You can put this solution on YOUR website! x intercept of 11 is (11,0)
y-intercept of -2 is (0.-2)
The slope of that line is -2/-11 or 2/11
It passes through (0,-2), so the equation is y=(2/11)x-2
--------------------------------
The slope of f is the negative reciprocal of 2/11 or -11/2
It has a point of (-4,8)
slope intercept form os y-y1=m(x-x1), where m is the slope, and (x1,y1) is a point
y-8=(-11/2)(x+4)
y-8=(-11/2)x-22
y=(-11/2)x+14
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Write the slope-intercept equation of the function f whose graph satisifies the given conditions.
The graph of f passes through
left parenthesis negative 4 comma 8 right parenthesis(−4,8)
and is perpendicular to the line that has an x-intercept of
11
and a y-intercept of
negative 2−2.
|
|
|
| |
