|
Question 1044739: Tickets are sold at $4.00 for adults and $2.50 for students. If 100 tickets were sold for $355.00, how many tickets were adult tickets? I need to define the variable, state the system and answer the question.
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
Tickets are sold at $4.00 for adults and $2.50 for students. If 100 tickets were sold for $355.00,
how many tickets were adult tickets? I need to define the variable, state the system and answer the question.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Variables: let "x" be the numbers of adult tickets, and
let "y" be the numbers of student tickets.
The system is:
x + y = 100, (1) ("100 tickets were sold") and
4x + 2.5y = 355. (2) ("100 tickets were sold for $355.00")
To solve the system, express "x" from (1): x = 100 - y, and substitute it into (2). You will get a single equation for y:
4*(100 - y) + 2.5y = 355.
Simplify and solve it:
400 - 4y + 2.5y = 355, or
-1.5y = 355 - 400,
-1.5y = -45,
y = 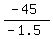 = 30.
So, we just found y, the number of student tickets.
Then x = 100 - y = 100 - 30 = 70. It is the number of adult tickets.
Check: 70*4 + 30*2.5 = 280 + 75 = 355. Correct !
Answer. 70 adult and 30 student tickets were sold.
|
|
|
| |
