Question 1044331: Line L has a slope of -3. The line through which of the following pair of points is perpendicular to L.
a. (-2,-3), (-3,-6)
b. (-18,-1),(-3,0)
c. (-4,-3), (-3,-6)
d. (-6,-4), (-3,-3)
How can I solve this?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! equation of a line is:  where where  is slope and is slope and  is y-intercept is y-intercept
if given line  has a slope of has a slope of  , means , means 
the line perpendicular to L will have slope a negative reciprocal of  and it is and it is 

now check given choices:
a. ( , , ), ( ), ( , , ) )

 -> true, so pair of points ( -> true, so pair of points ( , , ), ( ), ( , , ) is on a line perpendicular to L ) is on a line perpendicular to L
b. (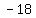 , , ), ( ), ( , , ) )

 -> not true, so pair of points ( -> not true, so pair of points (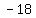 , , ), ( ), ( , , ) is not on a line perpendicular to L ) is not on a line perpendicular to L
c.
( , , ), ( ), ( , , ) )

 -> not true, so pair of points ( -> not true, so pair of points ( , , ), ( ), ( , , ) is not on a line perpendicular to L ) is not on a line perpendicular to L
d.
( , , ), ( ), ( , , ) )

 -> not true, so pair of points ( -> not true, so pair of points ( , , ), ( ), ( , , ) is not on a line perpendicular to L ) is not on a line perpendicular to L
so, option a. ( , , ), ( ), ( , , ) is your answer ) is your answer
|
|
|