Draw the boundary line for the inequality 2x+2y > 6, which
has the equation the same as the inequality with the >
replaced by an =.
2x+2y = 6 has x-intercept (3,0) and y-intercept (0,3)
Draw it dotted because the inequality is > and not ≥.
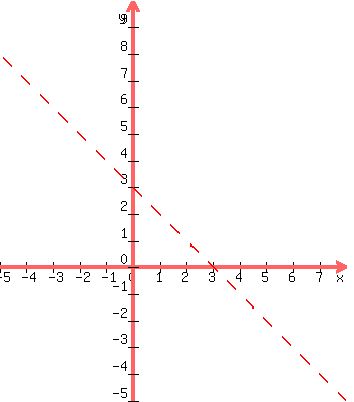Test to see if the origin (0,0) is a solution. If it is, then
all the solution points are on the same side of the line as
the origin is on. Otherwise they are all on the side the origin
is NOT on. We substitute the origin (x,y) = (0,0) in
2x+2y > 6
2(0)+2(0) > 6
0 > 6
That's false, so we know the solutions are all on the side the
origin is NOT on, so we know that we'll be shading above and to
the right of the line, for that's the side that the origin is
NOT on.
Next we draw the boundary line for the inequality x < 5, which
has the equation the same as the inequality with the <
replaced by an =.
That's x = 5 which is a vertical line through 5 on the x-axis.
Draw it dotted because the inequality is < and not ≤.
Test to see if the origin (0,0) is a solution. If it is, then
all the solution points are on the same side of the line as
the origin is on. Otherwise they are all on the side the origin
is NOT on. We substitute the origin (x,y) = (0,0) in
x < 5
We only need to substitute 0 for x since there is no y in the
equation:
0 < 5
That's true, so we know the solutions are all on the side the
origin IS on, so we know that we'll be shading to the left of
the vertical line, for that's the side that the origin IS on.
Next we draw the boundary line for the inequality y ≥ 5, which
has the equation the same as the inequality with the ≥
replaced by an =.
That's y = -2 which is a horizontal line through -2 on the y-axis.
Draw it solid because the inequality is ≥ and not >.
Test to see if the origin (0,0) is a solution. If it is, then
all the solution points are on the same side of the line as
the origin is on. Otherwise they are all on the side the origin
is NOT on. We substitute the origin (x,y) = (0,0) in
y ≥ -2
We only need to substitute 0 for y since there is no x in the
equation:
0 ≥ -2
That's true, so we know the solutions are all on the side the
origin IS on, so we know that we'll be shading above the
horizontal line, for that's the side that the origin IS on.
Actually this line does not change the solution since we shade
above it anyway. So we shade above the slanted line, to the
left of the vertical line, which is of course above the
horizontal line, so the finished graph is:
Edwin
