|
Question 1030378: I'm not really sure which section this question would fall under. It's a story problem, and honestly I have no idea where to even begin. I've had great help from the tutors in this section, so I thought I would try again.
the reflector of a flashlight is in the shape of a paraboloid of revolution. its diameter is 4 inches and its depth is 1 inch. How far from the vertex should the light bulb be placed so that the rays will be reflected parallel to the axis?
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I'm not really sure which section this question would fall under. It's a story problem, and honestly I have no idea where to even begin.
I've had great help from the tutors in this section, so I thought I would try again.
The reflector of a flashlight is in the shape of a paraboloid of revolution.
Its diameter is 4 inches and its depth is 1 inch.
How far from the vertex should the light bulb be placed so that the rays will be reflected parallel to the axis?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since you have a problem "where to begin", start reading the lesson
Parabola definition, canonical equation, characteristic points and elements in this site.
We are given that the diameter of the paraboloid of revolution is 4 inches and its depth is 1 inch.
It means that if we consider the parabola as the section of the given paraboloid, it has the equation
y = 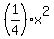 (y = 1 at x = 2). Hence, the parameter "p" in the equation (1) of the referred lesson is equal to 2: p = 2.
OK. Surely, we will place the light bulb in the focus of the parabola to use its optical property,
and we need to determine the distance from the focus to the parabola vertex.
According to the general theory (see the lesson referred above), the focus is located at the distance
(y = 1 at x = 2). Hence, the parameter "p" in the equation (1) of the referred lesson is equal to 2: p = 2.
OK. Surely, we will place the light bulb in the focus of the parabola to use its optical property,
and we need to determine the distance from the focus to the parabola vertex.
According to the general theory (see the lesson referred above), the focus is located at the distance  from the vertex.
So, the distance under the question is from the vertex.
So, the distance under the question is  = = 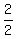 = 1 inch.
Answer. The light bulb should be placed at the distance 1 inch from the paraboloid vertex. = 1 inch.
Answer. The light bulb should be placed at the distance 1 inch from the paraboloid vertex.
|
|
|
| |