Question 1023756: linear equations with substitution and graphing-
3x-y=2
-6x+2y=6
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! In how many ways can six students be seated in a row of 6 desks?
Suppose the students are A, B, C, D, E, and F
a) if two of the six students insist on sitting
next to each other
Suppose the students who insist on sitting next
to each other are A and B.
Then there are two cases of arranging 5 "things"
in a row.
Case 1: The 5 "things are AB, C, D, E, and F
That's 5!
Case 2: 5 "things are BA, C, D, E, and F
That's also 5!
Answer 5! + 5! = 120 + 120 = 240 ways.
b) if two of the six students refuse to sit next
to each other
First we find the number of ways they can sit
without restrictions:
That's 6! = 720
Then we subtract the 240 ways from the first
part of the problem:
720 - 240 = 480 ways.
Edwin
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Substitution:
 --> -->
Substituting the expression 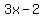 for for  in in  we get we get
 --> --> ---> --->
Since  is not true for any pair of (x,y) values, is not true for any pair of (x,y) values,
the system has no solution.
It is "inconsistent".
Of course, you could also have simplified the second equation:
 --> --> --> --> , or , or
 --> --> --> --> , which would have shown the system is inconsistent, , which would have shown the system is inconsistent,
because 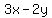 cannot be equal to cannot be equal to  and to and to  at the same time. at the same time.
Graphing:
 obviously passes through point (0,-2), obviously passes through point (0,-2),
because when  , ,  . .
When  , ,  --> --> --> --> --> --> , ,
so  also passes through point (1,1). also passes through point (1,1).
Plotting points (0,-2) and (1,1), and connecting them with a straight line we get the graph for  . .
 obviously passes through (0,3), obviously passes through (0,3),
because  --> --> --> --> , ,
and through (-1,0),
because  -->-6x=6}}}--> -->-6x=6}}}-->
Plotting points (0,3 and (-1,0), and connecting them with a straight line we get the graph for  . .
The graph for the system is
 The lines are parallel, so there is no point (x,y) that belongs to both lines,meaning that there is no solution. The lines are parallel, so there is no point (x,y) that belongs to both lines,meaning that there is no solution.
You can be sure that the lines are parallel because the have the same slope=3, as x increases by 1, y increases by 3.
Both lines make the same angle with the x-axis, and with all the gridlines parallel to the x-axis, as you can see from the red right triangles below:

|
|
|