Question 1003267: Two lines are perpendicular if Line 1 through (-4, 1) and (-2, -3) and Line 2 through (2, 1)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given:
Two lines are perpendicular: means their slopes are negative reciprocals to each other
if the slope of line 1 is  , then the slope of line 2 is , then the slope of line 2 is 
Line 1 through ( , ,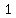 ) and ( ) and ( , , ): ):
find the slope-intercept form of the equation or  for this line using given points for this line using given points
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (-4, 1) and (x2, y2) = (-2, -3).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(-2)x + (-7)
Your graph:

|
so, your line 1 has equation  , and its slope is , and its slope is 
now find negative reciprocal 


so far the equation of line 2 is 
since given that Line 2 through ( , ,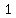 ) =( ) =( , ,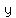 ), use this point to find ), use this point to find 




now we have the equation of line 2:  or or 
see them on a graph:

|
|
|