|
Question 995643: Find the distance between the pair of parallel lines.
y= 4x + 4
y= 4x - 4
Answer options: a)2.01 b)2.2 c)1.94 d)2.37
This was from a recent math test I took and I can't figure out how to solve. I have a chapter test coming up and want to prepare.
Found 3 solutions by josgarithmetic, MathLover1, MathTherapy:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! 


to find the distance between the pair of parallel lines first find perpendicular line and its intersection points with given parallel lines
given parallel lines have same slope and it is 
y-intercept of first line is at ( , , ) and ) and
y-intercept of second line is at ( , , ) )
so, the perpendicular line will have a slope negative reciprocal to  and it is and it is 
use the slope and y-intercept of first line is at ( , , ) to find the equation of the line perpendicular to the line ) to find the equation of the line perpendicular to the line 
The equation of the line that has that  and goes through point ( and goes through point ( , , ) is: ) is:



so, the lines  and and  are perpendicular to each other and intersect at ( are perpendicular to each other and intersect at ( , , ) )
now we need to find intersection point of the lines  and and 
equal right sides and solve for 









with corresponding  , ,


so, the lines  and and  intersect at ( intersect at (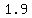 , ,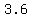 ) )

now, find the distance between points ( , , ) and ( ) and (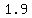 , ,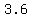 ); that will be the distance between given parallel lines ); that will be the distance between given parallel lines







so, your answer is c)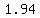
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the distance between the pair of parallel lines.
y= 4x + 4
y= 4x - 4
Answer options: a)2.01 b)2.2 c)1.94 d)2.37
This was from a recent math test I took and I can't figure out how to solve. I have a chapter test coming up and want to prepare.
The distance between these 2 lines is the perpendicular line drawn to both lines
Slope of perpendicular line to y = 4x + 4 or y = 4x - 4: 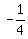
1) Using this slope and point (0, 4), determine the equation of the line that's equidistant from these 2 lines
2) Determine the point at which the perpendicular line intersects the line: y = 4x - 4
3) With the two coordinate points where the perpendicular line intersects both lines, use the distance formula to find the distance between the 2 lines
4) You should get distance as: 1.938501 ≈ 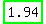 (CHOICE c) (CHOICE c)
|
|
|
| |