|
Question 990689: Please my good genius Algebra.Com help me with this !Find the equation of the tangent to the circle x^2 + y^2 + ax + 2ay = 3 at the point (0, b) in terms of a and b. If this tangent has a gradient of 1/4,find the relation between a and b. Hence, find the equations of the two possible circles.
Answer by anand429(138)   (Show Source):
You can put this solution on YOUR website! Equation of circle is
=> 
=> 
So the center of circle is
(-a/2, -a) and radius is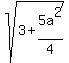 
Slope of radius at (0,b) = 
=2(a+b)/a
SO slope of tangent at (0,b) = (-a/(2(a+b))) (Since radius and tangent are perpendicular and so product of their slopes will be -1)
So let equation of tangent be
Since it passes through (0,b)
So,
b=(-a/(2(a+b)))*0 + c
=> b=c
So the equation of tangent becomes,
 --------------Required equation of tangent
If this tangent has a gradient of 1/4
then,
=> 
=>  ----(i) ----------------Required relation between a and b
Also, since (0,b) lies on circle,So
0^2 + b^2 + a*0 + 2ab =3
=> b^2 + 2ab - 3 = 0
Putting value of b from eqn. (i) above,
9a^2 -6a^2 - 3 =0
=> a^2 =1
=> a=1 or a = -1
Putting these values of a in original equations of circle, we get
and
as two equations of possible circles.
|
|
|
| |
