|
Question 938101: Two vertices of an equilateral triangle are (3,4)and (-2,3) the third vertex can be
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two vertices of an equilateral triangle are (3,4)and (-2,3) the third vertex can be
-------------
The distance between the given points is sqrt(26)
----
Draw circles or radius sqrt(26) with the given points as centers.
The 2 intersections of the circles are the 2 possible 3rd vertices.
===========
email via the TY note for help or to check your work.
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two vertices of an equilateral triangle are (3,4)and (-2,3) the third vertex can be
There are obviously two solutions:
 and and  First we find the distance between them to find out the
lengths of the three sides of the equilateral triangle.
First we find the distance between them to find out the
lengths of the three sides of the equilateral triangle.




 Let the third vertex be the point (u,v)
Then the distance from (u,v) to (3,4) must
equal to the distance from (u,v) to (-2,3),
and each must equal to
Let the third vertex be the point (u,v)
Then the distance from (u,v) to (3,4) must
equal to the distance from (u,v) to (-2,3),
and each must equal to  . .
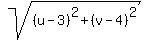  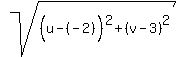   Squaring all three sides:
Squaring all three sides:
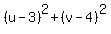  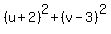  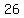
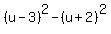  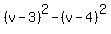
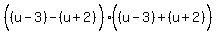  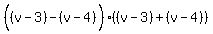
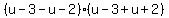  
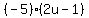  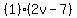
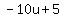  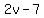
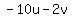  
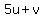  
 Substitute in
Substitute in
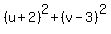  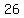
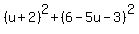  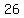
  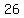











 ----
Using the +,
----
Using the +,






 ,
so one solution is ,
so one solution is 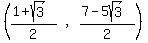 , which is about (-0.4,7.8)
----
Using the -, , which is about (-0.4,7.8)
----
Using the -,






 ,
so the other solution is ,
so the other solution is  , which is about (1.4,-0.8)
Edwin , which is about (1.4,-0.8)
Edwin
|
|
|
| |