SOLUTION: a jet plane travelling at 500 mph over takes a propeller plane travelling at 200 mph that had a 2-hour head start.how far the starting point are the planes?

Algebra ->  Length-and-distance -> SOLUTION: a jet plane travelling at 500 mph over takes a propeller plane travelling at 200 mph that had a 2-hour head start.how far the starting point are the planes?      Log On


   

Question 930541: a jet plane travelling at 500 mph over takes a propeller plane travelling at 200 mph that had a 2-hour head start.how far the starting point are the planes?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
A jet plane travelling at J mph over takes a propeller plane travelling at P mph that had a k hour head start.how far the starting point are the planes?


J=500, P=200, k=2.
Let d be the distance each travels by the time both went the same distance (and meet);
Let t be the time that the faster plane (jet) traveled until caught up to the slower plane.


__________________rate________time_________distance
JET_______________J____________t____________d
PROP______________P___________t+k___________d

Two variables, but the variable to solve for is d. First you can solve for t if you want. Maybe not the only way.

system%28Jt=d%2CP%28t%2Bk%29=d%29


Solve for t in terms of d, no matter which equation you start with.
t=d%2FJ;
;
P%28t%2Bk%29=d
P%28d%2FJ%2Bk%29=d
Pd%2FJ%2BPk=d
Pd%2FJ-d=-Pk
d%28P%2FJ-1%29=-Pk
highlight%28d=%28-Pk%29%2F%28P%2FJ-1%29%29
which you could simplify further...
d=%28-PkJ%29%2F%28P-J%29
in which you may check that P-J is a negative value...
d=%28%28-PJk%29%2F%28P-J%29%29%28%28-1%29%2F%28-1%29%29
highlight%28d=%28PJk%29%2F%28J-P%29%29


Evaluate d for the specific exercise using the given values.

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!

a jet plane travelling at 500 mph over takes a propeller plane travelling at 200 mph that had a 2-hour head start.how far the starting point are the planes?
Upon overtaking the propeller plane, the jet and propeller planes would’ve traveled the same distance

Let the distance traveled by both planes, to the meeting point, be D

Then time taken by propeller plane to travel to planes’ meeting point = 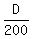D%2F200

Time taken by jet plane to travel to planes’ meeting point = 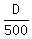D%2F500

We therefore have: D%2F200+=+D%2F500+%2B+2

5D = 2D + 2,000 ------- Multiplying by LCD, 1,000

5D – 2D = 2,000

3D = 2,000

D, or distance traveled by the planes, or distance from starting point = 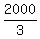2000%2F3, or highlight_green%28666%262%2F3%29 miles

You can do the check!! 

===================

Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.

Further help is available, online or in-person, for a fee, obviously. 



For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams,GENERAL

MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra, 

Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,

GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.