|
Question 927826: Find the distance between the two parallel lines 2x-3y=4 and 2x-3y=-4
I was told there was a formula for this, but I cannot seem to find it.
Thank you
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! You could say there is a formula but you do not need it. You could try to derive a formula, or you could just pick any point on either of the two given lines, find where a line intersects both of these and passes through you chosen point.
The two given lines have slope of  . Any line perpendicular to them will have slope  . Try to put either equation into slope-intercept form if you not see this.
Pick an equation and find an axis intercept.
One point on this line is (2,0), which is x-intercept for 2x-3y=4.
The line containing (2,0) and with slope , using point-form to start, is 
You want to find what point is the intersection of this line with the second given line of  .
Solve this second equation for y:
-
Equate the expressions of y for the perpendicular equation and the given second equation:
LCD is 6;
Multiply left and right by 6;
 ----seems inconvenient.....
Use x to find y:
-
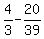
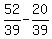
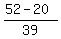
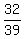
Point on this second line is (32/39, -10/13).
LAST, use the Distance Formula to find the distance between the points, (32/39, -10/39) and (2,0).
(Process and final result not here shown...)
|
|
|
| |
