|
Question 849726: Find the distance between the two parallel lines given by the equation: 5x-4y=22 and -75x=150-60y
the instructions given by the teacher were:
1. put both equations in y=mx+b form
2. find a point (x,y) on either equation
3. find equation of the perpendicular line that passes through (x,y)
4. use systematic equation to solve with equation 3 (the new one) and the one that wasn't used to get the point in step 2
5. calculate with distance formula
I don't know how to continue after solving both equations for y=mx+b
Found 2 solutions by Alan3354, josgarithmetic:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the distance between the two parallel lines given by the equation: 5x-4y=22 and -75x=150-60y
----------------
5x-4y=22 --> y = (5/4)x - 11/2
-75x=150-60y --> y = (5/4)x + 5/2
------------
y = (5/4)x - 11/2
(0,-11/2) is a point
Perpendicular thru the point --> y = (-4/5)x - 11/2
-----
y = (-4/5)x - 11/2 = (5/4)x + 5/2
-16x - 110 = 25x + 50
x = -160/41
y = 640/205 - 11/2 = 256/82 - 451/82 = -195/82
Intersection at (-160/41,-195/82)
--------------
d =~ 4.95
Answer by josgarithmetic(39617)  (Show Source):
You can put this solution on YOUR website! 5x-4y=22 and -75x=150-60y
1. put both equations in y=mx+b form
2. find a point (x,y) on either equation
3. find equation of the perpendicular line that passes through (x,y)
4. use systematic equation to solve with equation 3 (the new one) and the one that wasn't used to get the point in step 2
5. calculate with distance formula
(The statement of your number 4 is not in the best wording).
BOTH EQUATIONS INTO SLOPE-INTERCEPT FORM
 ----first equation
-
 ----second equation
PICK ANY POINT ON ONE EQUATION
y=(5/4)x+5/2
Let x=2.
y=(5/4)*2+5/2
y=5/2+5/2
y=5.
Point picked is (2, 5).
LINE PERPENDICULAR CONTAINING (2, 5):
Arbitrary choice to use point-slope formula.
Want slope  .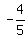
 ----Perpendicular to both of the given equations
INTERSECTION OF and :
Obvious formulas for y are expected equal if the two equations intersect.
Multiply members by 20 which is LCD.
(25+16)x=110+132=242
-
Find y.
-
POINT on first equation is ( 242/41, 483/41 ).
FINDING DISTANCE BETWEEN THE TWO FOUND POINTS
Step 5 on your list.
You want to use the distance formula to determine or find what is the distance between ( 242/41, 483/41 ) and (2, 5).
Very possibly, if you would try to make a graph of the two given lines, you MIGHT find more convenient set of points to use, such as to pick a point on either line and possibly have a more convenient point on the other line, intersecting also a more convenient perpendicular to both.
-
Distance is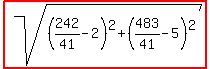 
|
|
|
| |
