|
Question 844782: A ball is tossed in the air from an initial height of 6 feet, it reaches its maximum height of 10 feet after 3 seconds then comes back down.then it bounces back up to a second maximum height of 1 foot in 1 second
a) Assume that the motion is parabolic in each case and determine a piecewise function h(t). express all non- exact answers rounded correctly to three decimal places.
b) now assume that the whole time it is doing this, it is moving in the horizontal(call it the x direction) at a constant speed of 1.5 feet per second. Determine the particles path through space h(x(t)) as a piecewise function as it goes through the initial toss and two bounces leave all non-exact answers rounded to three decimal places.
guys I need help in home work :) i would appreciate the help
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem reads as a math problem, so I will forget that I know physics.
a) Assuming that the motion is parabolic, we expect the pieces of the graph of  as a function of as a function of  to look like this: to look like this:
 The first piece has axis of symmetry The first piece has axis of symmetry  seconds, seconds,
apex/vertex at  feet, feet,
and  feet. feet.
From  , a flip, a vertical stretch, and a translation bring us to , a flip, a vertical stretch, and a translation bring us to
 as a candidate function. as a candidate function.
That function graphs as a parabola with a vertex at  seconds with seconds with  feet. feet.
We know that we need 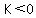 for the vertex to be a maximum, and that we need for the vertex to be a maximum, and that we need  feet. feet.






So the first piece of the function, from  to the first bounce point, where to the first bounce point, where  is is

 --> --> --> --> --> --> --> --> --> --> --> --> seconds = approx. seconds = approx.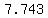 seconds . seconds .
So the first piece is
 } for } for  seconds . seconds .
The second bounce takes the ball up to  foot 1 second later,at foot 1 second later,at
 seconds, and parabola symmetry requires that the ball get back to seconds, and parabola symmetry requires that the ball get back to  in another second at in another second at  seconds. seconds.
The function  goes from goes from  to a maximum of to a maximum of  in 1 second. in 1 second.
We need the same shape, but shifted right so the vertex is at  instead of instead of  . .
So  for for  would cover the second piece of the piecewise function. would cover the second piece of the piecewise function.
b)  <--> <-->  <--> <--> 
We can express the trajectory function 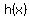 by substituting by substituting  into into  . .
The  part of the piecewiese function corresponds to part of the piecewiese function corresponds to  <--> <-->

and we get  . .
For the second piece,  corresponds to corresponds to
 <--> <-->
and we get

However, using the more accurate  value, we get value, we get
 when rounded to 3 decimal places. when rounded to 3 decimal places.
So  for for  . .
IN REVENGE
for making me calculate a bunch of ugly numbers,
I want to point out that the problem is really out of this world.
The acceleration of the ball after it was tossed in the air was
 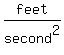 , but on my planet the acceleration of gravity is , but on my planet the acceleration of gravity is   . .
On earth's moon, it would be   . .
That ball is being tossed on a quite small satellite or asteroid, with little gravity.
after it bounces, the acceleration suddenly increases to
  . .
That is even stranger, because gravity should remain constant on any planet, satellite, or asteroid.
It would have been more consistent if the bounce had made the ball reach 1 foot is 1.5 seconds. Then the acceleration of gravity before and after the bounce would have been the same.
|
|
|
| |