SOLUTION: How do I determine the point(s) where the line {{{y=mx}}} intersects with the circle {{{x^2+y^2=4}}} so far i have managed to figure out the positive intersect but not the negativ

Algebra ->  Length-and-distance -> SOLUTION: How do I determine the point(s) where the line {{{y=mx}}} intersects with the circle {{{x^2+y^2=4}}} so far i have managed to figure out the positive intersect but not the negativ      Log On


   

Question 790833: How do I determine the point(s) where the line y=mx intersects with the circle x%5E2%2By%5E2=4
so far i have managed to figure out the positive intersect but not the negative point
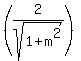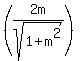
to find the positive one I subbed y=mx in to x%5E2%2By%5E2=4 isolated and solved to find the point %282%2Fsqrt%281%2Bm%5E2%29%29,%282m%2Fsqrt%281%2Bm%5E2%29%29
any help is very appreciated
Answer by tinbar(133) About Me  (Show Source):
You can put this solution on YOUR website!
Not sure how you found one without the other but your idea is correct.
x^2 + y^2 = 4
x^2 + (mx)^2 = 4 ... since y = mx
x^2 + m^2*x^2 = 4
x^2(1 + m^2) = 4
x^2 = 4 / (1 + m^2)
Now from here if you take (positive) +sqrt(4/1+m^2)) you get the solution you have already presented, that is, x = 2/(sqrt(1 + m^2)), and then you plugged this into the expression y = mx, to get y = 2m/(sqrt(1 + m^2)) which is correct. Now to get your second solution you take the (negative) -sqrt(4/1+m^2)) to ultimately get the second solution of x = -2/(sqrt(1 + m^2)) and y = -2m/(sqrt(1 + m^2)).
Explanation for second solution: Anytime you have something like x^2 = blah blah blah, then when you undo the square on the left side by taking square root, that is only one solution, the second solution comes from taking the negative version. Consider x^2 = 4. Solving for x here is solving the square root of 4. What is the square root of 4? 2 obviously, BUT also -2. Why? Because negative times negative is a positive!
Now think about this a bit more and consider what happens when we increase the power for x, that is, what are ALL the solutions to the following cases:
a) x^2 = 4. Solutions are +2 and -2
b) x^3 = 8.
c) x^4 = 16 ... this one is trickier, the solutions are not just +2 and -2. Consider the special number i = sqrt(-1). Notice that i = sqrt(-1) implies i^2 = -1 which implies (i^2)^2 = (-1)^2 = 1... Using this new notion of "i" can you find more solutions for part b? In fact, try to find a pattern between the number of solutions (including those involving "i") and the power corresponding to x (which is called the "degree")