SOLUTION: a point is at a distance 4 sqrt of 2 units from (-3/2,-5/2) and at a distance 2 sqrt of 5 units from (9/2,-5/2), find the point

Algebra ->  Length-and-distance -> SOLUTION: a point is at a distance 4 sqrt of 2 units from (-3/2,-5/2) and at a distance 2 sqrt of 5 units from (9/2,-5/2), find the point      Log On


   

Question 774946: a point is at a distance 4 sqrt of 2 units from (-3/2,-5/2) and at a distance 2 sqrt of 5 units from (9/2,-5/2), find the point
Found 2 solutions by Alan3354, josgarithmetic:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
a point is at a distance 4 sqrt of 2 units from (-3/2,-5/2) and at a distance 2 sqrt of 5 units from (9/2,-5/2), find the point
-----------
Draw a circle around each given point with the radius = the given distance.
The points (2 of them) will be the intersections of the circles.
---
a distance 4 sqrt of 2 units from (-3/2,-5/2) --> %28x+%2B+3%2F2%29%5E2+%2B+%28y+%2B+5%2F2%29%5E2+=+32
a distance 2 sqrt of 5 units from (9/2,-5/2) --> %28x+-+9%2F2%29%5E2+%2B+%28y+%2B+5%2F2%29%5E2+=+20
-----------
Lucky the y terms are equal
%28x+%2B+3%2F2%29%5E2+%2B+%28y+%2B+5%2F2%29%5E2+=+32
%28x+-+9%2F2%29%5E2+%2B+%28y+%2B+5%2F2%29%5E2+=+20
------------------------------ Subtract
%28x+%2B+3%2F2%29%5E2+-+%28x+-+9%2F2%29%5E2+=+12
%282x+%2B+3%29%5E2+-+%282x+-+9%29%5E2+=+48
%284x%5E2+%2B+12x+%2B+9%29+-+%284x%5E2+-+36x+%2B+81%29+=+48
48x+-+72+=+48
x = 5/2
--------
Sub for x into either eqn, find 2 values for y

Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
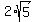[ a point is at a distance 4sqrt%282%29 units from (-3/2,-5/2) and at a distance 2%2Asqrt%285%29 units from (9/2,-5/2), find the point ]

This point is unknown (x,y).

Look for one or two triangles with one side 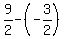9%2F2-%28-3%2F2%29 units long, and two other sides which are the two given lengths:
--------------------------------------------
4%2Asqrt%282%29=sqrt%28%28x-%28-3%2F2%29%29%5E2%2B%28y-%28-5%2F2%29%29%5E2%29
4%2Asqrt%282%29=sqrt%28%28x%2B3%2F2%29%5E2%2B%28y%2B5%2F2%29%5E2%29
highlight%2832=%28x%2B3%2F2%29%5E2%2B%28y%2B5%2F2%29%5E2%29_______We can make more use of this one.
which is a circle

2%2Asqrt%285%29=sqrt%28%28x-9%2F2%29%5E2%2B%28y-%28-5%2F2%29%29%29
highlight%2820=%28x-9%2F2%29%5E2%2B%28y%2B5%2F2%29%5E2%29_______ .
also a circle

These two circles both contain the expression 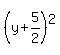%28y%2B5%2F2%29%5E2, which give us a way to relate them.
32-%28x%2B3%2F2%29%5E2=20-%28x-9%2F2%29%5E2
%28x-9%2F2%29%5E2-%28x%2B3%2F2%29%5E2-20+%2B32=0
x%5E2-%2818%2F2%29x%2B81%2F4-%28x%5E2%2B%286%2F2%29x%2B9%2F4%29%2B12=0
x%5E2-9x%2B81%2F4-%28x%5E2%2B6x%2B9%2F4%29%2B12=0
-9x%2B81%2F4-6x-9%2F4%2B12=0
-15x%2B12%2B72%2F4=0
-15x%2B12%2B18=0
15x=30
highlight%28x=2%29

What you now want to do, is go back to this same circle equation, solve it for y, and assign x=2 and find the value for y. You will get two solutions for this y. Whatever y is found to be, the two points wanted will be (2, y) and (2, -y).