|
Question 742526: Indicate the equation of the given line in standard form.
The line containing the median of the trapezoid whose vertices are R(-1, 5) , S(1, 8), T(7, -2), and U(2, 0).
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
first draw the median of the trapezoid; find endpoints:
| Solved by pluggable solver: Midpoint |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (-1, 5), we can say (x1, y1) = (-1, 5)
So  , , 
Since the second point is (1, 8), we can also say (x2, y2) = (1, 8)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
----------------------------------------------------------------------------------------
Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 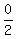
X Coordinate of Midpoint = 
So the x coordinate of the midpoint is 0
----------------------------------------------------------------------------------------
Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2
Y Coordinate of Midpoint = 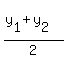
Y Coordinate of Midpoint = 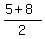
Y Coordinate of Midpoint = 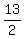
Y Coordinate of Midpoint = 
So the y coordinate of the midpoint is 6.5
===============================================================================
Summary:
The midpoint of the segment joining the two points (-1, 5) and (1, 8) is (0, 6.5).
So the answer is (0, 6.5)
|
| Solved by pluggable solver: Midpoint |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (2, 0), we can say (x1, y1) = (2, 0)
So  , , 
Since the second point is (7, -2), we can also say (x2, y2) = (7, -2)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
----------------------------------------------------------------------------------------
Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 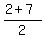
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
So the x coordinate of the midpoint is 4.5
----------------------------------------------------------------------------------------
Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2
Y Coordinate of Midpoint = 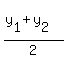
Y Coordinate of Midpoint = 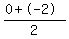
Y Coordinate of Midpoint = 
Y Coordinate of Midpoint = 
So the y coordinate of the midpoint is -1
===============================================================================
Summary:
The midpoint of the segment joining the two points (2, 0) and (7, -2) is (4.5, -1).
So the answer is (4.5, -1)
|
so, endpoints are: (0, 6.5) and (4.5, -1)
now find the equation of a line containing the median of the trapezoid
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (0, 6.5) and (x2, y2) = (4.5, -1).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(-1.66666666666667)x + (6.5)
Your graph:

|
all together:

and, the equation of a line in standard form is: 
|
|
|
| |