You don't need the Pythagorean theorem.
Given ߡABC with vertices A(-1,2), B(5,-4), C(9,6), prove that CD
is both an altitude (perpendicular to base AB) and a median
(bisects the base) where D is the point D(-4,3).
Draw ߡABC and AD
 We need to show that
(1) CD ⊥ AB and (2) D is the midpoint of AB.
For (1), we find the slopes of CD and AB and show that they are negative
reciprocals, that their product is -1.
Slope formula:
m =
We need to show that
(1) CD ⊥ AB and (2) D is the midpoint of AB.
For (1), we find the slopes of CD and AB and show that they are negative
reciprocals, that their product is -1.
Slope formula:
m =  To find the slope of CD:
where (x1,y1) = C(6,8)
and where (x2,y2) = D(-4,3)
m =
To find the slope of CD:
where (x1,y1) = C(6,8)
and where (x2,y2) = D(-4,3)
m = 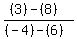 =
= 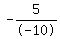 =
=  To find the slope of AB:
where (x1,y1) = A(-6,7)
and where (x2,y2) = B(-2,-1)
m =
To find the slope of AB:
where (x1,y1) = A(-6,7)
and where (x2,y2) = B(-2,-1)
m = 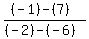 =
= 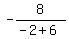 =
= 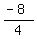 = -2
Since
= -2
Since  and
and  are negative reciprocals,
their product is -1, we have proved that CD ⊥ AB,
which proves that CD is an altitude to base AB.
For (2), we use the midpoint formula to show that D(-4,3) is the
midpoint of AB.
Midpoint formula:
Midpoint =
are negative reciprocals,
their product is -1, we have proved that CD ⊥ AB,
which proves that CD is an altitude to base AB.
For (2), we use the midpoint formula to show that D(-4,3) is the
midpoint of AB.
Midpoint formula:
Midpoint =  where (x1,y1) = A(-6,7)
and where (x2,y2) = B(-2,-1)
Midpoint =
where (x1,y1) = A(-6,7)
and where (x2,y2) = B(-2,-1)
Midpoint =  =
= 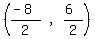 = (-4,3) which is point D.
Thus CD is also a median to the base AB of ߡABC.
Edwin
= (-4,3) which is point D.
Thus CD is also a median to the base AB of ߡABC.
Edwin