SOLUTION: segment AB with endpoints A=(-4,-6) AND b=(5,1) a.Find the midpoint of AB. b.Find the slope of the containing A and B c.Find AB please explain it step by step and how you got t

Algebra ->  Length-and-distance -> SOLUTION: segment AB with endpoints A=(-4,-6) AND b=(5,1) a.Find the midpoint of AB. b.Find the slope of the containing A and B c.Find AB please explain it step by step and how you got t      Log On


   

Question 698437: segment AB with endpoints A=(-4,-6) AND b=(5,1)
a.Find the midpoint of AB.
b.Find the slope of the containing A and B
c.Find AB
please explain it step by step and how you got the answer.
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

midpoint will be
Solved by pluggable solver: To find midpoint of segment connecting two point
The Coordinates of mid point of a line segment joining two points can be calculated using following formulas.

X coordinate of mid point is

X%5Bmid%5D=+%28X+coordinate_of_first_point+%2B+X+coordinate_of_first_point%29%2F2


X%5Bmid%5D+=%28-4%2B5%29%2F2


X%5Bmid%5D+=%28-4%2B5%29%2F2=0.5


Y coordinate of mid point is

Y%5Bmid%5D=+%28Y+coordinate_of_first_point+%2B+Y+coordinate_of_first_point%29%2F2


Y%5Bmid%5D+=%28-6%2B1%29%2F2


Y%5Bmid%5D=%28-6%2B1%29%2F2=-2.5

Hence, The mid point of segment joining two point (-4,-6) and (5,1) is (0.5,-2.5)



a. the midpoint of AB is at (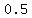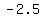0.5,-2.5)

b.Find the slope
first find the equation of a line that passes through given points


Solved by pluggable solver: FIND EQUATION of straight line given 2 points
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (-4, -6) and (x2, y2) = (5, 1).
Slope a is .
Intercept is found from equation a%2Ax%5B1%5D%2Bb+=+y%5B1%5D, or 0.777777777777778%2A-4+%2Bb+=+-2.88888888888889. From that,
intercept b is b=y%5B1%5D-a%2Ax%5B1%5D, or b=-6-0.777777777777778%2A-4+=+-2.88888888888889.

y=(0.777777777777778)x + (-2.88888888888889)

Your graph:




the slope is
m=0.777777777777778 or rounded m=0.8


c.Find AB
first find the distance between A and B, it will be answer to c

Solved by pluggable solver: Distance between two points in two dimensions
The distance (denoted by d) between two points in two dimensions is given by the following formula:

d=sqrt%28%28x1-x2%29%5E2+%2B+%28y1-y2%29%5E2%29

Thus in our case, the required distance is
d=sqrt%28%28-4-5%29%5E2+%2B+%28-6-1%29%5E2%29=+11.4017542509914+


For more on this concept, refer to Distance formula.


so, AB=11.4