SOLUTION: Solve for x in the equation x + 1 = the square root of (the total of) x + 3. Thank you very much. Sabin

Algebra ->  Length-and-distance -> SOLUTION: Solve for x in the equation x + 1 = the square root of (the total of) x + 3. Thank you very much. Sabin       Log On


   

Question 59927: Solve for x in the equation x + 1 = the square root of (the total of) x + 3.
Thank you very much.
Sabin
Found 2 solutions by funmath, praseena:
Answer by funmath(2933) About Me  (Show Source):
You can put this solution on YOUR website!
Hi Sabin,
Solve for x in the equation x + 1 = the square root of (the total of) x + 3.
x%2B1=sqrt%28x%2B3%29
%28x%2B1%29%5E2=%28sqrt%28x%2B3%29%29%5E2
x%5E2%2B2x%2B1=x%2B3
x%5E2%2B2x-x%2B1-3=x-x%2B3-3
x%5E2%2Bx-2=0
(x+2)(x-1)=0
x+2=0 and x-1=0
x+2-2=0-2 and x-1+1=0+1
x=-2 and x=1
Check for extraneous soltuions.
1%2B1=sqrt%281%2B3%29
2=sqrt%284%29
2=2 x=1 checks out.
-2%2B1=sqrt%28-2%2B3%29
-1=sqrt%281%29
-1=1 x=-2 is extraneous.
The only solution is x=1
Happy Calculating!!!

Answer by praseena(37) About Me  (Show Source):
You can put this solution on YOUR website!
x+1=squr(x+3)
squaring on both sides, we have
(x+1)^2=x+3
expanding the expression (x+3)^2, we have,
x^2+2x+1=x+3
subtracting 3 on both sides,
x^2+2x-2= x
subtracting x from both sides
x^2+x-2=0, which is of the form x^2+bx+c=0, which can be solved using the formula, x=%28-b%2B_sqrt%28b%5E2-4%2Aa%2Ac%29%29%2F%282%2Aa%29
here, a=1 b=1 and c= -2
substitute these values in the given formula we havw,
x = 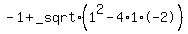-1%2B_sqrt%281%5E2-4%2A1%2A-2%29%29%2F2%2A1
which comes like this
x = -1+_sqrt(1+8)/2
= (-1+_sqrt(9)/2
= (-1+_3)/2
which is either, x = (-1+3)/2 or x=(-1-3)/2

so x=2/2=1 or x=-4/2=-2
so x=1 or-2