|
Question 388591: (I hope that I'm putting this in the right category)
(ignore the numbers)Points(Clock-wise): S(-a, b); P(a, b); Q(a, -b); R(-a, -b)
a. (find missing coordinates. I when ahead and provided all coordinates.)
b. Find the length of the diagonals
c. Describe your results in part (b) as a theorem.
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! S(-a, b); P(a, b); Q(a, -b); R(-a, -b)
S(-2,2);P(2,2);Q(2,-2);R(-2,-2)
a. (find missing coordinates. I when ahead and provided all coordinates.)
b. Find the length of the diagonals
S(-2,2);Q(2,-2);
Distance formula
D=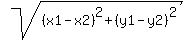 
D=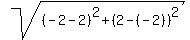 
...
D=
...
 the diagonal length
...
(-2,-2),P(2,2);
Since these pointsform a square the other diagonal will also have same length.
...
m.ananth@hotmail.ca
|
|
|
| |
