|
Question 203426: A wooden board is placed so that it leans against a loading dock to provide a ramp. The board is supported by a metal beam perpendicular to the ramp and placed on a 1 ft. tall support. The bottom of the support is 8 feet from the point where the ramp meets the ground. The slope of the ramp is 2/5 (this means that for every 2 feet it goes up, it goes 5 to the side). Find the length of the beam to the nearest hundredth of a foot. Note that the 1 ft. support is vertical, but the metal beam is not.
Remember a slope of 2/5 means that everytime you go horizontal 5 units, you go vertical 2 units. (So at 10 units, it should be vertical 4 units, and at 15 it should be vertical 6 units, etc.) Also remember that perpendicular lines have an opposite slope...so if a line has a slope of 1/3, then its perpendicular line will have a slope of -3/1.
Find the distances and plot the points, so you can use the distance formula on the points on either side of the metal beam to find its length! Look for any possible way to find the information you need!
Do the problem step by step, showing your work and explaining what you did to find the answer (the drawings here will help, but make your own--you do not need to submit your drawing, you only need to use it for your own reference). On three of the steps, "prove" what you're doing by stating the theorem or definition you're working with. (You must have three separate proofs--using the distance formula three times doesn't count!)
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Ground is represented by  line. line.
Ramp is represented by 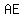 , support by , support by  and beam by and beam by  . .
According to given conditions, support BC is perpendicular to ground at B and beam CD is perpendicular to ramp at D.
The coordinates of all the points are mentioned in the diagram.
Let the coordinates of the point D be (p,q).
Since, the slope of the ramp is 2/5 so equation to ramp AE is 5x - 2y = 0.
The equation to beam CD, perpendicular to AE, is of the form 2x + 5y + k = 0 where k = constant.
To find k, we note that this line passes through C whose coordinates are (8,1).
So equation for CD must be satisfied by substituting x=8 and y=1.
Thus, we have 2*8 + 5*1 + k = 0 i.e. k = -21.
So, equation for CD is 2x + 5y - 21 = 0
D is the point of intersection of lines AE and CD. To find its coordinates we must solve the equations of those lines.
Solve:
5x - 2y = 0 and
2x + 5y -21 = 0
Solution: x = 7.2414, y = 2.8965
Hence, p = 7.2414, q = 2.8965
Now,length of the CD = 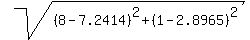 = 2.0426. = 2.0426.
Thus, the length of the beam is 2.0426 feet.
|
|
|
| |