SOLUTION: Find the radius of a circle with center at (4,1) if a chord of length 4 times square root of 2 is bisected at (7,4).

Let O be the center of the circle (4,1).
Let P be the point (7,4), 
Let A and B be the endpoints of the chord,
so the chord is the segment AB. Draw the
graph:



Draw in OA and OP:



We need to find the length of OA since it 
is a radius of the circle.

Triangle OPA is a right triangle, since if a
bisector of a chord passes through the center of
a circle, then it is perpendicular to the chord.

We are given that chord AB has length ,
and since P bisects it, then AP is half that length
or .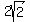

Next we will find the length of OP by use of the
distance formula:



using the given coordinates of O(4,1) and P(7,4):











Now by the Pythagorean theorem,













And since OA is a radius, the circle has 
radius .

Edwin