SOLUTION: the point(x,4) is a square root of 162 units from (-6,-5). What is the value of abscissa x?

Algebra ->  Length-and-distance -> SOLUTION: the point(x,4) is a square root of 162 units from (-6,-5). What is the value of abscissa x?      Log On


   

Question 166143: the point(x,4) is a square root of 162 units from (-6,-5). What is the value of abscissa x?
Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!

Distance from 2 set of points:
highlight%28D%5E2=%28x%5B2%5D-x%5B1%5D%29%5E2%2B%28y%5B2%5D-y%5B1%5D%29%5E2%29
Given: points ------> (x,4)(-6,-5)
Distance=sqrt%28162%29
Subst.
%28sqrt%28162%29%29%5E2=%28-6-x%29%5E2%2B%28-5-4%29%5E2, cancels out "square root" on the left term
162=x%5E2%2B12x%2B36%2B%28-9%29%5E2
x%5E2%2B12x%2B36%2B81-162=0
x%5E2%2B12x-45=0, SOLVE BY PYTH. THEOREM
where----system%28a=1%2Cb=12%2Cc=-45%29
Then, x=%28-b%2B-sqrt%28b%5E2-4ac%29%29%2F%282a%29
x=%28-12%2B-sqrt%2812%5E2-4%2A1%2A-45%29%29%2F%282%2A1%29
x=%28-12sqrt%28144%2B180%29%29%2F2
x=%28-12%2B-sqrt%28324%29%29%2F2=%28-12%2B-18%29%2F2
2 Values:
x=%28-12%2B18%29%2F2=6%2F2=cross%286%293%2Fcross%282%291 ---> highlight%28x=3%29, abscissa
Also, x=%28-12-18%29%2F2=-30%2F2=cross%28-30%2915%2Fcross%282%29 --> x=-15
We'll use highlighted ---> x=3, for the graph below:
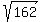---> See the BLUE Line @ points (3,4) & (-6,-5) that has distance of sqrt%28162%29.
.
With points (3,4) & (-6,-5), will it equate to Distance=sqrt%28162%29? Let's see:
With our Distance formula, we'll find 1st x%5B2%5D & x%5B1%5D:

---> As you see on the graph, x%5B2%5D=3 & x%5B1%5D=-6, good!
Next we find y%5B2%5D & y%5B1%5D, and as we see the graph:

---> As you can see, y%5B2%5D=4 & y%5B1%5D=-5:
By then, going back to our formula:
D%5E2=%28x%5B2%5D-x%5B1%5D%29%5E2%2B%28y%5B2%5D-y%5B1%5D%29%5E2
%28sqrt%28162%29%29%5E2=%283-%28-6%29%29%5E2%2B%284-%28-5%29%29%5E2
162=%283%2B6%29%5E2%2B%284%2B5%29%5E2
162=9%5E2%2B9%5E2=81%2B81
162=162, good!
*Our dimensions are right.
Thank you,
Jojo