SOLUTION: I need help with a question could someone please help?? Find the length, to the nearest tenth, of the apothem of a regular octogon whose sides are each 10 inches long?

Algebra ->  Length-and-distance -> SOLUTION: I need help with a question could someone please help?? Find the length, to the nearest tenth, of the apothem of a regular octogon whose sides are each 10 inches long?      Log On


   

Question 165933: I need help with a question could someone please help??
Find the length, to the nearest tenth, of the apothem of a regular octogon whose sides are each 10 inches long?
Found 2 solutions by MRperkins, Edwin McCravy:
Answer by MRperkins(300) About Me  (Show Source):
You can put this solution on YOUR website!
Question: Find the length, to the nearest tenth, of the apothem of a regular octagon whose sides are each 10 inches long.
.
Answer: The center of a regular polygon is equidistant from the vertices. The apothem is the distance from the center to a side. A central angle of a regular polygon has its vertex at the center, and its sides pass through consecutive vertices.
.
Each central angle measure of a regular n-gon is 360%2Fn degrees.
.
Draw the octagon. Draw an isosceles triangle with its vertex at the center of the octagon. The central angle is 360%2F8 or 45 degrees. Draw a segment that bisects the central angle and the side of the polygon to form a right triangle.
.
Use the tangent ratio to find the apothem
tan22.5=5%2Fa The tangent of an angle is %22tangent_angle%22=%22opposite_leg%22%2F%22adjacent_leg%22.
*NOTE: you use 22.5 because you bisected the central angle
a=%285%2F%28tan22.5%29%29 Solve for a.
a=8.96295... inches Round to the nearest tenth
a=9.0 inches
.
Check out my website by clicking on my profile.
You can find a scanned picture of my work for this problem. Just go to the solutions page and click on "apothem"
.
contact justin.sheppard.tech@hotmail.com with any questions

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Edwin's solution:
Warning: MRperkins's solution is correct up to the last step.
He apparently mis-pressed something on his calculator and got
the wrong answer. Here is my complete solution with drawings:
I need help with a question could someone please help??

Find the length, to the nearest tenth, of the apothem of a regular octogon whose sides are each 10 inches long?
  
Draw the octagon, all sides of which are 10 inches.
I'll just indicate that the bottom side is 10:
 

Now temporarily, connect the vertices
to the center:

I did that just to show that each
of those 8 angles at the center are
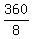360%2F8%29° = 45°, so that if we
erase all but the bottom two, like this:



Now we know that the angle in the
above is 45°


Now draw in an apothem, the line from
the center to the midpoint of the bottom
 side, and label it a.


Since the sides
of the octagon are 10 each, the two parts of
the bottom side are 5 each. Also the 45° angle
is bisected into two angles which are 22.5° each




So lets take away everything but
just this little right triangle:



Then we just do a little trig on that triangle:

The side opposite the 22.5° angle is 5 and the
side adjacent to it is a, so

tan%2822.5%29=5%2Fa

Multiply both sides by a:

a%2Atan%2822.5%29=5

Divide both sides by tan(22.5°):

a=5%2Ftan%2822.5%29

a=12.07106781

or, to the nearest tenth,

a=12.1 inches.

Edwin