|
Question 152310: 26.) The midpoint of the line segment joining a moving point to (6,0) is on the line y=x. Find the equation of its locus.
Ans. x-y+6=0
This is a question that comes with the answer but I don't know how to solve for it. I tried using the midpoint formula but the answer is either x+y-6=0 or x-y-6=0. I don't know how to solve for this kind of problem...
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! 26.) The midpoint of the line segment joining a moving point to (6,0) is on the line y=x. Find the equation of its locus.
Ans. x-y+6=0
Graph the line  : :
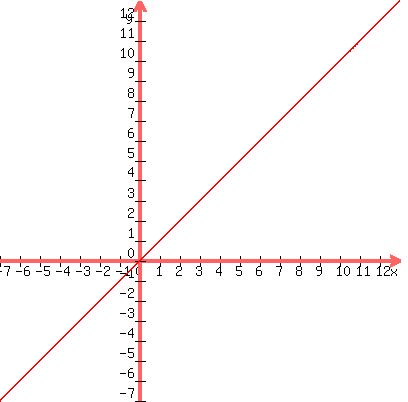 Call point (6,0) the point R.
Draw an arbitrary line from point R(6,0), crossing the
line
Call point (6,0) the point R.
Draw an arbitrary line from point R(6,0), crossing the
line  at point M, and extending to P so that MP
equals RM. making M the midpoint of RP. P is the moving
point. at point M, and extending to P so that MP
equals RM. making M the midpoint of RP. P is the moving
point.
 Label the moving point P with the variable coordinates (x,y)
Label the moving point P with the variable coordinates (x,y)
 Since point M is the midpoint of the line segment RP, we use
the midpoint formula to label M with the coordinates
(
Since point M is the midpoint of the line segment RP, we use
the midpoint formula to label M with the coordinates
(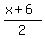 , ,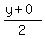 ) or ( ) or (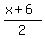 , , ) )
 Now the point M(
Now the point M(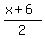 , , ) is on the line ) is on the line  , so
it must satisfy the equation , so
it must satisfy the equation  , so we substitute that point
into the equation , so we substitute that point
into the equation  and we get: and we get:
 Multiply both sides by 2:
Multiply both sides by 2:
 That is equivalent to
That is equivalent to
 To see the path of the moving point we draw the graph of
To see the path of the moving point we draw the graph of
 in green in green
 Edwin
Edwin
|
|
|
| |