SOLUTION: I think I use the Pythagorean thoerem to solve this problem, but I really have no clue... I appreciate any help you can offer.. Here's the problem: While finding the amount of se

Algebra ->  Length-and-distance -> SOLUTION: I think I use the Pythagorean thoerem to solve this problem, but I really have no clue... I appreciate any help you can offer.. Here's the problem: While finding the amount of se      Log On


   

Question 142617This question is from textbook University of Phoenix
: I think I use the Pythagorean thoerem to solve this problem, but I really have no clue... I appreciate any help you can offer..
Here's the problem:
While finding the amount of seed needed to plant his three square wheat field, George observed that the side of one field was 1 kilometer longer than the side of the smallest field and that the side of the largest field was 3 kilometers longer than the side of the smallest field. If the total area of the 3 fields is 38 kilometers, then what was the area of each field???
Thanks sooo much!! This question is from textbook University of Phoenix

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Nope, Pythagoras won't be of much help on this one.

George has three differently sized square fields. Since they are square, you know that the area of each of the fields is the length of the side of that field squared.

Let the length of the side of the smallest field be x, so the area of the smallest field is x%5E2.

The length of the side of the middle-sized field is 1 km longer than the length of the side of the smallest field, so the length of the side of the middle-sized field must be x+%2B+1. Therefore the area of the middle-sized field must be %28x+%2B+1%29%5E2

Likewise, the length of the side of the largest field must be 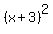x+%2B+3 and the area must be %28x+%2B+3%29%5E2

The total area, given as 38km%5E2, has to be the sum of these three areas. So:

x%5E2%2B%28x%2B1%29%5E2%2B%28x%2B3%29%5E2=38

Now all you need to do is expand the binomials, collect like terms, put the equation into standard quadratic form, and then solve the quadratic equation. There will be 2 roots to the equation, one of which will be a negative number. Since we are looking for a positive measure of length, you can exclude the negative root as extraneous. The other root is the length of the side of the smallest field, from which you can calculate the area. Use the expressions developed for the area of the other two fields to calculate their areas.

Hint: The quadratic IS factorable, but a little tricky. Don't struggle too long with it. If you don't see the factorization right away, use the quadratic formula.