SOLUTION: ABCD is a trapezoid with BC perpendicular to AB and BC perpendicular to CD, AB = 13, BC = 12, and CD = 8. A line segment is drawn from A to E, the midpoint of CD. a. Find the ar

Make the drawing below. We are given that BC = 12, and since
E is given as the midpoint of CD, which is 8, then CE and ED are 4 each.  

 

Draw EF parallel to BC, then EF = BC = 12, and
since BF = CE = 4 and AB = 13, then by subtraction,
AF = AB - BF = 13 - 4 = 9:

 

We can find the area of trapezoid AFED using the
formula

        /b1 + b2\
Area = |---------|h 
        \  2    /


Area of trapezoid AFED =  =  =  =  =  

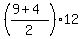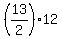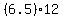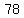We can find the area of triangle AFE using the 
formula:

Area = {{(bh)/2}}} =  =  =  =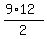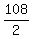 

Now since

Area of trapezoid AFED = Area of triangle AFE + Area of triangle AED

                    78 = 54 + Area of triangle AED

so Area of triangle AED = 78 - 54 = 24

So that's the answer to part a.

------------------------------------------

Now we must find the perimeter of triangle AED.

We have one side of it, DE, which is 4.

We can find side AE for it is the hypotenuse of right triangle AFE.

We use the Pythagorean theorem

c² = a² + b²

AE² = AF² + EF² = 9² + 12² = 81 + 144 = 225

so  =  =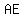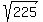 

Now we only need side DA.

To do this we need to draw DG parallel to BC and EF.

then DG = EF = BC = 12, and
since GF = DE = 4 and AF = 9, then by subtraction,
AG = AF - GF = 9 - 4 = 5:



We can find side AD for it is the hypotenuse of right triangle AGD.

We use the Pythagorean theorem

c² = a² + b²

AD² = AG² + DG² = 5² + 12² = 25 + 139 = 169

so  =  = 

Now the perimeter of triangle AED is the sum of
its three sides:

Perimeter = AE + DE + AD = 15 + 4 + 13 = 32

Edwin