Discussion
The basic formula for this sort of problem is 
.
But it seems at first glance that there isn't enough information.
What we need to do is create two relationships that express the time it took to
travel one direction in terms of the given distance, 4 miles, and the rate in
still water.
So we are going to use the distance formula in this configuration: 
Solution
Let's let the rate in still water (the value we are trying to determine)
be 
. Since we know that the rate of the current was 5 mph, the boat
would go 5 mph slower than the rate in still water going upstream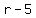 
,
and 5 mph faster than the rate in still water going downstream 
.
Let's say that the time it took to go downstream is t, and we are given that
the time upstream was 40 minutes longer. 40 minutes is 2/3 hour, so we can
express the upstream time as 
.
Using the distance/rate/time formula solved for time, we can write:
to describe the downstream trip and
to describe the upstream trip
Taking the second equation and adding 
to both sides,
Now, since we have two things equal to t, we can set them equal to each other.
Add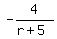 
to both sides to get everything on the left set equal to 0
Now we have three rational expressions. To obtain the sum, we need a lowest
common denominator. Since there are no factors in common among the three
denominators, the LCD is simply the product of the three, namely:
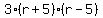
So, applying this LCD, we have:
This looks rather ugly, but it's not as bad as it looks. Remember that 
,
if and only if 
and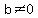 
.
Just to make sure the denominator is never zero, we need to exclude any
result of 5 or -5, but for the moment, all we need to to is simplify the
numerator, set it equal to zero, and solve.
roughly 9.2 mph
Check Answer
Downstream trip: 
, rationalizing the denominator:
Upstream trip: 
, rationalizing the denominator:
These two times should differ by 2/3, so:
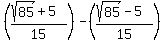
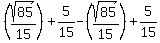
, answer checks.
(