SOLUTION: Line \ell_1 represents the graph of 3x + 2y = -14. Line \ell_2 passes through the point (0,0), and is perpendicular to line \ell_1. Write the equation of line \ell_2 in the form

The commonly known fact is that if you have a line

    ax + by = c,


then a perpendicular line is

    -bx + ay = d   (where "a", "b", "c" and "d" are constant values).


Using it, we see that in our case an equation of the desired line is

    -2x + 3y = d    (where d is some constant).


And since this line should pass through (0,0),  d = 0.


Thus, the desired equation is

    3y = 2x,


or, in the form y = ax+b, it is

    y = 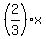.    ANSWER