SOLUTION: Hi, can you help me solve this problem? Given a quadrilateral whose vertices are ( 3, 5 ) , ( 4, -1 ), ( 8, -2 ) and ( 9, 7 ), show that the line segments joining the midpoints

Algebra ->  Length-and-distance -> SOLUTION: Hi, can you help me solve this problem? Given a quadrilateral whose vertices are ( 3, 5 ) , ( 4, -1 ), ( 8, -2 ) and ( 9, 7 ), show that the line segments joining the midpoints       Log On


   

Question 1197664: Hi, can you help me solve this problem?
Given a quadrilateral whose vertices are ( 3, 5 ) , ( 4, -1 ), ( 8, -2 ) and ( 9, 7 ), show
that the line segments joining the midpoints of adjacent sides from a parallelogram.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
Hi, can you help me solve this problem?
Given a quadrilateral whose vertices are ( 3, 5 ) , ( 4, -1 ), ( 8, -2 ) and ( 9, 7 ), show
that the line segments joining the midpoints of adjacent sides from a parallelogram.
~~~~~~~~~~~~~~~ 

This statement is true for ANY convex quadrilateral on a plane:


    for any convex quadrilateral on a plane, the segments joining
    the midpoints of adjacent sides form a parallelogram.


The proof is in couple of lines.


    Draw one diagonal of the parallelogram.

    Then two of the four listed segments are midlines in the two triangles.
    Therefore, these two segments are parallel to that diagonal and,
    hence, are parallel to each other.


    Same reasoning works for other two segments and the other diagonal.


    Thus, these segments are in-pair parallel as opposite sides 
    of the drawn quadrilateral, proving that the drawn quadrilateral,
    consisting of these segments is a parallelogram.

The statement is proved and the proof is completed.

------------

See the lesson
    - Midpoints of a quadrilateral are vertices of the parallelogram
in this site.

Also,  you have this free of charge online textbook on Geometry
    GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.

The referred lesson is the part of this online textbook under the topic  "PROPERTIES OF PARALLELOGRAMS".


Save the link to this online textbook together with its description

Free of charge online textbook in GEOMETRY
https://www.algebra.com/algebra/homework/Triangles/GEOMETRY-your-online-textbook.lesson

to your archive and use it when it is needed.



Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
I'll do all but the last two steps.



We use the midpoint formula to find the midpoints of the sides:

Midpoint =  

Midpoint of the top side:

Midpoint = %28matrix%281%2C3%2C%283%2B9%29%2F2%2C+%22%2C%22%2C%285%2B7%29%2F2%29%29 =
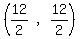
           %28matrix%281%2C3%2C12%2F2%2C+%22%2C%22%2C12%2F2%29%29
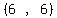           %28matrix%281%2C3%2C6%2C+%22%2C%22%2C6%29%29

Midpoint of the left side:

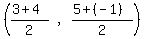Midpoint = %28matrix%281%2C3%2C%283%2B4%29%2F2%2C+%22%2C%22%2C%285%2B%28-1%29%29%2F2%29%29 =
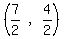
           %28matrix%281%2C3%2C7%2F2%2C+%22%2C%22%2C4%2F2%29%29
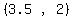           %28matrix%281%2C3%2C3.5%2C+%22%2C%22%2C2%29%29

Midpoint of the bottom side:

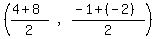Midpoint = %28matrix%281%2C3%2C%284%2B8%29%2F2%2C+%22%2C%22%2C%28-1%2B%28-2%29%29%2F2%29%29 =
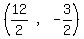
           %28matrix%281%2C3%2C12%2F2%2C+%22%2C%22%2C-3%2F2%29%29
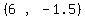           %28matrix%281%2C3%2C6%2C+%22%2C%22%2C-1.5%29%29

Midpoint of the right side:

Midpoint = %28matrix%281%2C3%2C%288%2B9%29%2F2%2C+%22%2C%22%2C%28-2%2B7%29%2F2%29%29 =
           %28matrix%281%2C3%2C17%2F2%2C+%22%2C%22%2C5%2F2%29%29
           %28matrix%281%2C3%2C8.5%2C+%22%2C%22%2C2.5%29%29



Now we just need to show that the two pairs of opposite sides are parallel
by showing that the pairs have the same slope.

We use the slope formula:

m%22%22=%22%22%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (6,6)
and where (x2,y2) = (3.5,2)
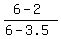
m%22%22=%22%22%286-2%29%2F%286-3.5%29
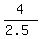m%22%22=%22%224%2F%282.5%29%22%22=%22%221.6%29

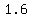We find the slope of its opposite side

m%22%22=%22%22%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (6,-1.5)
and where (x2,y2) = (8.5,2.5)
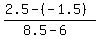
m%22%22=%22%22%282.5-%28-1.5%29%29%2F%288.5-6%29
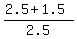
m%22%22=%22%22%282.5%2B1.5%29%2F2.5
m%22%22=%22%22%284%29%2F%282.5%29%22%22=%22%221.6%29

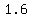So that shows that those two green sides are parallel,
since their slopes are both 1.6.

I'm going to stop here and let you finish on your own by
showing that the slopes of the other pair of opposite sides 
are also parallel, by showing that they have the same slope 
also, by the same method.

The problem will not be complete until you do this last part.

Edwin