|
Question 1195043: Two sides of a triangle field measure 325 meters and 278 meters. If these sides form an angle of 47°40’, what is the length of the fence that will surround the field?
Found 3 solutions by ikleyn, ankor@dixie-net.com, MathTherapy:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
Use the cosine law formula to find third side of the triangle field,
opposite to the given angle.
Then add the lengths of the three sides of the triangle to find its perimeter,
which is, OBVIOUSLY, the length of the fence surrounding the field.
Happy calculations (!)
Answer by ankor@dixie-net.com(22740)  (Show Source):
You can put this solution on YOUR website! Two sides of a triangle field measure 325 meters and 278 meters.
If these sides form an angle of 47°40’, what is the length of the fence that will surround the field?
:
Find the side opposite the angle
Change 47' 40" to 47 + 40/60 = 47.67 degrees
use the law of cosines here: a^2 = b^2 + c^2 - 2bc Cos(A) where,
a = side opposite 47.67 degrees
b = 325 m
c= 278 m
A = 47.67 degrees
:
a^2 = 325^2 + 287^2 - 2(325*287) Cos(27.67)
a^2 = 105625 + 82369 - 186550 * .8856
a^2 = 187994 - 125662.7
a =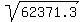 
a = 249.7 meters is the 3rd side
then
325 + 287 + 249.7 = 861.7 meters to surround the field
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website! Two sides of a triangle field measure 325 meters and 278 meters. If these sides form an angle of 47°40’, what is the length of the fence that will surround the field?
Using law of cosines, we get: 
You now have the 3 sides (a, b, and c) of the triangle. I take it you know how to calculate the perimeter of this triangle, correct?
|
|
|
| |
