|
Question 1195042: A vertical pole on a 15° slope is braced by a wire from the top of the pole to a point 20 ft. uphill from the base. If the pole subtends an angle of 62°30' from this point. Find the height of the pole and length of the wire.
Answer by ikleyn(52914)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A vertical pole on a 15° slope is braced by a wire from the top of the pole
to a point 20 ft. uphill from the base. If the pole subtends an angle of 62°30'
from this point, find the height of the pole and length of the wire.
~~~~~~~~~~~~~~~
Let point A be the base of the pole;
point B be the upper end of the pole,
and point C be the point where the wire is attached to the slope of the hill.
We have triangle ABC with this given information:
- angle C is 62°30';
- angle A is 90° - 15° = 75°;
- side AC is 20 ft long.
They want you find side c = AB (the pole height) and the side a = BC (the length of the wire).
First, we find the measure of the angle B: it is 180° - 62°30' - 75° = 42°30'.
Next, write sine law proportion
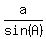 = = 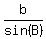 = = 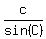 .
To find side c = AB, use this part of the proportion .
To find side c = AB, use this part of the proportion
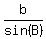 = = 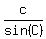 , , 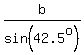 = = 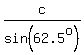 , , 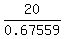 = = 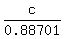 ,
which gives c = ,
which gives c = 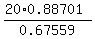 = 26.26 ft (the height of the pole). ANSWER
To find side a = BC, use this part of the proportion = 26.26 ft (the height of the pole). ANSWER
To find side a = BC, use this part of the proportion
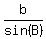 = = 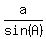 , , 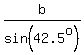 = = 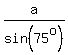 , , 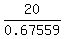 = = 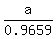 ,
which gives a = ,
which gives a = 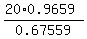 = 28.59 ft (the length of the wire). ANSWER = 28.59 ft (the length of the wire). ANSWER
Solved.
|
|
|
| |