SOLUTION: Two poles have wires running from the top of each to the base of the base of the other. If the poles are 8 m and 12 m high, at what height do the wires cross?

Click here to see ALL problems on Length-and-distance

Question 1190310: Two poles have wires running from the top of each to the base of the base of the other. If the poles are 8 m and 12 m high, at what height do the wires cross?
Found 3 solutions by math_tutor2020, Alan3354, greenestamps:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Let's say we had these four points
A = (0,0)
B = (0,8)
C = (p,0)
D = (p,12)
I'll make p > 0, but it easily works for negative values of p as well.
The only condition really is that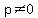

Joining points A and B gets segment AB which is the first tower (8 meters)

Joining points C and D gets segment CD which is the second tower (12 meters)

The distance between the base of each tower (A and C) is exactly p units.
It will turn out that the value of p doesn't matter.

Let's find the equation of line BC
m = slope
m = (y2-y1)/(x2-x1)
m = (0-8)/(p-0)
m = -8/p
The y intercept of line BC is b = 8 because of point B on the y axis.
y = mx+b
y = (-8/p)x+8

The equation of line BC is: y = (-8/p)x+8

Through similar steps, the equation of line AD is y = (12/p)x

Let point E be the intersection of those two lines. The goal is to find the y coordinate of point E.

-----------------------------------------

Apply substitution to get
y = (-8/p)x+8
(12/p)x = (-8/p)x+8
12x = -8x + 8p
12x+8x = 8p
20x = 8p
x = 8p/20
x = 2p/5

Then plug this into either equation for BC or AD
y = (-8/p)*x + 8
y = (-8/p)*(2p/5) + 8
y = -16/5 + 8
y = -16/5 + 40/5
y = (-16 + 40)/5
y = 24/5
y = 4.8
Or
y = (12/p)*x
y = (12/p)*(2p/5)
y = 24/5
y = 4.8

Either way we get y = 4.8 as the height of the intersection of the two lines.

In either case, the p variables cancel out.
This means that the horizontal distance between the poles doesn't matter.

-----------------------------------------

Answer: 4.8 meters (this value is exact).

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
Two poles have wires running from the top of each to the base of the base of the other. If the poles are 8 m and 12 m high, at what height do the wires cross?
---------------
h = 8*12/(8+12) = 4.8 meters

Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

The answer from the first tutor uses algebra and equations of lines to solve the problem. That is a valid approach (and you should understand and be able to use it), but it is not very efficient.

The response from the other tutor gives you the right answer; but you learn nothing from it.

If you run into this kind of problem frequently -- e.g., if you compete in timed math competitions -- then this is a handy formula to memorize:

If the heights of the two towers are A and B, then the height where the wires cross is -- independent of the distance between the towers.

If you want to LEARN something about that formula, you can derive it using similar triangles.

Here is a diagram....

(1) Triangles CEF and CBA are similar:

(2) Triangles AEF and ADC are similar:

From (1) and (2),

Solve for y:

Multiply by the common denominator, without simplifying: