|
Question 1181253: Given Point P moving along curve y = x^2 - 1 and point Q moving along line y = x - 3, find the coordinates of point Q and the distance between P and Q when the distance between those two points is minimized.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given Point P moving along curve y = x^2 - 1 and point Q moving along line y = x - 3,
find the coordinates of point Q and the distance between P and Q
when the distance between those two points is minimized.
~~~~~~~~~~~~~~~
My common sense tells me that we should find the point on the parabola, where the tangent line
to the parabola is parallel to the given line, i.e. has the same slope of 1 as the given straight line.
Then the sough distance is the distance from this point to the line.
To find the point on the parabola with the slope of the tangent line equal to one,
take the derivative and equate it to 1
 = 2x = 1, which gives x= 0.5, y= 0.5^2 - 3 = 0.25 - 3 = -2.75.
To find the distance from the point (0.5,-2.75) to the line y = x-3, use the general formula for the distance
from the point (p,q) in the coordinate plane to the straight line Ax + By + C = 0.
This formula is d = = 2x = 1, which gives x= 0.5, y= 0.5^2 - 3 = 0.25 - 3 = -2.75.
To find the distance from the point (0.5,-2.75) to the line y = x-3, use the general formula for the distance
from the point (p,q) in the coordinate plane to the straight line Ax + By + C = 0.
This formula is d = 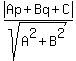 .
In our case, the equation of the line is x - y - 3 = 0, so A = 1, B = -1, C = -3, p= 0.5, q= -2.75.
We substitute these values into the formula (*) and get the answer
the distance d = .
In our case, the equation of the line is x - y - 3 = 0, so A = 1, B = -1, C = -3, p= 0.5, q= -2.75.
We substitute these values into the formula (*) and get the answer
the distance d = 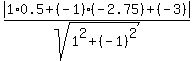 = = 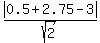 = = 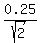 = = 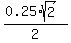 = = 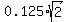 = 0.17678 (rounded).
ANSWER. The minimal distance is = 0.17678 (rounded).
ANSWER. The minimal distance is 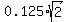 = 0.17678 (rounded). = 0.17678 (rounded).
Solved.
//////////////
Do not forget to post your "THANKS" to me for my teaching.
|
|
|
| |