|
Question 1173554: The equation used for converting degrees Celsius to degrees Fahrenheit is F=2C+30. (In function
notation this would be f(c)=2c +30 )
a) Find the inverse of this function.
Found 2 solutions by Theo, Solver92311:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the conversion factor you show is f = 2c + 30
to find the inverse of this function, replace f with c and c with f to get:
c = 2f + 30
you need to solve for f.
subtract 30 from both sides of the equation and then divide both side of the equation by 2 to get:
(c - 30) / 2 = f
switch sides to get:
f = (c - 30) / 2
to graph both functions, replace f with y and c with x.
the graphs looks like this:
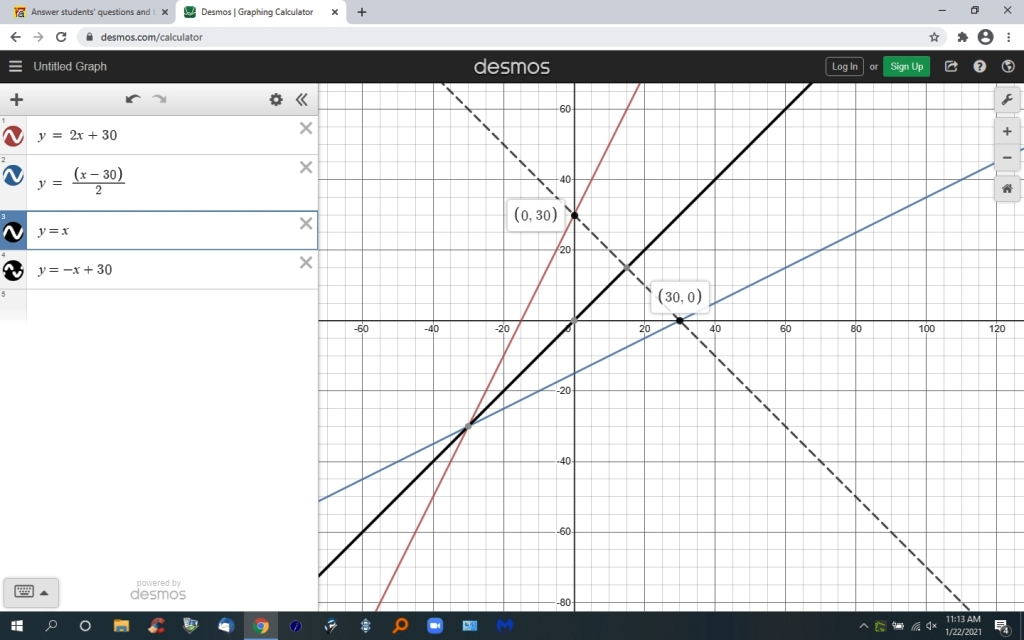
the original equation is y = 2x + 30.
that's in red.
when you replace y with f and x with c, the original equation becomes:
f = 2c + 30
the inverse equation is y = (x - 30) / 2
that's in blue.
when you replace y with f and x with c, the inverse equation becomes:
f = (c - 30) / 2
the line y = x is in black.
if the equations are inverses of each other, then they are reflections about the line y = x.
the dashed black line is y = -x + 30
that line is used to show the points directly opposite from each other about the line y = x.
the points are (0,30) on the original equation and (30,0) on the inverse equation.
this confirms the lines are reflections of each other about the line y = x.
another test is to use the composite function of f(g(x)) or g(f(x)) and get the value of x.
for example:
let f(x) = 2x + 30 and let g(x) = (x-30)/2
to get f(g(x)), replace x in f(x) with (x-30)/2 from g(x).
you will get:
f(g(x)) = 2 * (x-30)/2 + 30
simplify to get:'
f(g(x)) = 2 * x/2 - 2*30/2 + 30
simplify further to get:
f(g(x)) = x - 30 + 30
combine like terms to get:
f(g(x)) = x
to get g(f(x)), replace x in g(x) with (2x + 30) from f(x).
you will get:
g(f(x)) = ((2x + 30) - 30) / 2
simplify to get:
g(f(x)) = (2x) / 2
simplify further to get:
g(f(x)) = x
you got f(g(x)) = x and g(f(x)) = x
this confirms the equations are inverse of each other.
note that, if g(x) is inverse to f(x), then g(x) can also be written as f-1(x))
here's a reference on proving that the equations are inverse of each other.
https://www.purplemath.com/modules/invrsfcn7.htm
Answer by Solver92311(821)   (Show Source): (Show Source):
|
|
|
| |